
INVERSE EXPONENTIATED EXPONENTIAL POISSON DISTRIBUTION WITH THEORY AND APPLICATIONS
Lal Babu Sah Telee 1![]()
![]() ,
Vijay Kumar 2
,
Vijay Kumar 2![]()
1 Assistant
Professor, Department of Management Science, Nepal Commerce Campus, Tribhuvan
University, Kathmandu, Nepal
2 Professor, Department of Mathematics
and Statistics, Deen Dayal Upadhyaya, Gorakhpur University, Gorakhpur, India
|
|
ABSTRACT |
||
|
This paper is
based on new extension of the exponential distribution named “Exponentiated Exponential
Poisson Inverse (IEEP) distribution”. The distribution is based on lifetime
issues containing three parameters. Likelihood method is used to estimate the
parameters of the distribution. Explicit expressions for reliability/survival
function, the hazard rate function, reversed hazard rate, the quantile
function and mode are introduced. Maximum Likelihood estimates as well as
asymptotic confidence interval are obtained using theory of the Maximum
likelihood. For illustration and application, a real data set is analyzed and
compared with three other model of literature. Model fitted here is better
compared to other models for data considered. All the graphical and
computation analysis is performed using R programming. |
|||
|
Received 09 August 2023 Accepted 10 September 2023 Published 25 September 2023 Corresponding Author Lal Babu
Sah Telee, lalbabu3131@gmail.com DOI 10.29121/IJOEST.v7.i5.2023.535 Funding: This research
received no specific grant from any funding agency in the public, commercial,
or not-for-profit sectors. Copyright: © 2023 The
Author(s). This work is licensed under a Creative Commons
Attribution 4.0 International License. With the
license CC-BY, authors retain the copyright, allowing anyone to download,
reuse, re-print, modify, distribute, and/or copy their contribution. The work
must be properly attributed to its author.
|
|||
|
Keywords: Exponentiated Exponential Poisson Inverse, Exponential Distribution, Maximum Likelihood Estimation, Quantile, Hazard Rate |
|||
1. INTRODUCTION
Statistical distributions are the basic aspects of all parametric statistical techniques including inference, survival analysis, modelling and reliability etc. In recent years, new generate families of continuous models are derived. Lifetime problems can be solved by using the existing probability models but to get more precise result, we need some flexible probability models. Due to constant failure rate, exponential model cannot explain data with variable failure rate. Hence, misuse of exponential lifetime model will not be suitable. Here, our aim is to introduce a new three parameter lifetime distribution with strong physical motivations. At present many of new models are proposed by modifying, merging, and adding or removing some parameters in existing models Marshall and Olkin (2007). That is existing models can be defined in new family of distributions. Several techniques can be defined to form new family of distribution adding some extra parameters to the existing distributions Rinne (2009). and Pham and Lai (2007).
CDF of the continuous random variable X following
exponential distribution having constant ![]() is given as,
is given as,
![]() .
.
Some alternative generalizations of exponential distribution have been proposed to give some flexibility.
Although there are several generalizations of the exponential distributions, following two distributions have received more attention in literature with respect to others.
·
Marshall & Olkin (1997) introduced inventive
general method by adding some parameters to family of distributions which
states that X have the Marshall-Olkin extended exponential (MOEE) distribution,
say ![]() as
as
![]()
Here ![]() are called tilt and
scale constants. MOEE model reduces to exponential distribution for
are called tilt and
scale constants. MOEE model reduces to exponential distribution for ![]() equal to 1.
equal to 1.
·
Generalize: exponential (GE) distribution Gupta and Kundu (1999) can have
decreasing and right skewed with single mode value. Let X follows GE
distribution. That is![]() . The CDF of X is given by
. The CDF of X is given by
![]()
Above distribution has expression of the survival function like Weibull
distribution and properties similar to Gamma distribution.
To derive this model, we have used exponential distribution and the
Poisson distribution. Let us consider N system-based plant working
independently where N is truncated Poisson rv. Suppose each of the system
contains ![]() independent
and identically distributed units arranged in parallel. Suppose X is a random
variable defining time to fail the system Ristić & Nadarajah
(2014) and Kus (2007) then probability mass
function of the N will be.
independent
and identically distributed units arranged in parallel. Suppose X is a random
variable defining time to fail the system Ristić & Nadarajah
(2014) and Kus (2007) then probability mass
function of the N will be.
![]()
where n = 1, 2, 3…
Unconditional CDF of X having three parameters was introduced and was named as EEP Ristić & Nadarajah (2014) distribution
![]()
We have defined here three parameters Inverse Exponentiated
Exponential Poisson distribution (IEEP) taking inverse of random variable X
with CDF
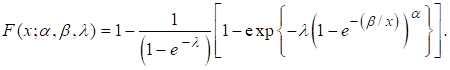
2. Model Analysis
2.1. Inverse Exponentiated exponential Poisson (IEEP) Distribution
Let X follows new extended exponential distribution then CDF of the
proposed model having three parameters is,
![]() (1)
(1)
2.2. Probability Density function
We defined model with pdf in expression as
![]() (2)
(2)
2.3. The Reliability function
It is defined as probability of not failing an event before given time t. Reliability function of IEEP is
![]() ; x > 0 (3)
; x > 0 (3)
2.4. The hazard rate (HRF)
Hazard function rate is defined as the instantaneous failure rate at time t. HRF of proposed model is
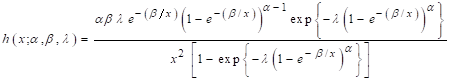 ;
x > 0 (4)
;
x > 0 (4)
Some of density function curves and hazard curves of IEEP using some of
values of![]() and
and ![]() are plotted in Figure 1 at constant value
of λ = 2 indicating that density curve of the IEEP is of different shapes
at different parameters values.
are plotted in Figure 1 at constant value
of λ = 2 indicating that density curve of the IEEP is of different shapes
at different parameters values.
Figure
1
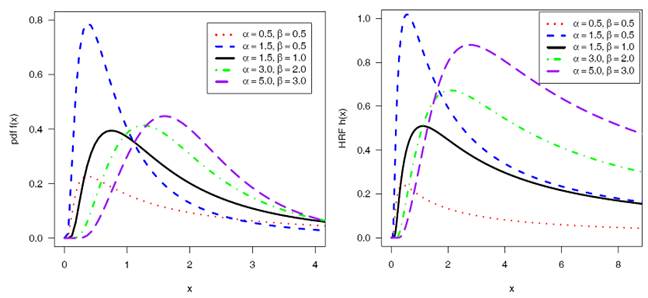
|
Figure 1 The PDF (Left) and
HRF(Right) of IEEP for Various Values of |
Behaviour of the hazard rate shows high flexibility for different
values of parameters. The HRF curve shows that the function is unimodal.
Function is monotonically increasing along with monotonically decreasing. It is
inverted bathtub hazard rates not showing constant hazard rates. We know that many of the lifetime’s
distribution does not show upside-down bathtub hazard rates, but it exhibits in
case of proposed model.
2.5. Statistical Properties
Major characteristics such as quantile function, skewness, and kurtosis etc of the proposed model IEEP are derived in this section.
2.6. Quantile Function
To study the theoretical aspect of probability model,
quantile function is used. Statistical measures like, partition values,
skewness as well as kurtosis of the probability models can be studied using
quantile function. Generating function of random variable can be expressed in
terms of quantile function. Quantile function can be used as the alternative
function of PDF and CDF for finding the nature of the distributions. Quantile
function of function can be obtained by using the relation![]() Quantile function for
model IEEP is,
Quantile function for
model IEEP is,
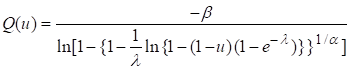 ; 0 < u < 1. (5)
; 0 < u < 1. (5)
U is uniform variate U (0, 1). If we put u = 0.5 in (5) then median will be obtained of the model can be obtained.
2.7. Asymptotic properties
This property of pdf the density function follows
condition of ![]() with the resulting
value as 0. That is, if both the limits converge to zero the proposed model
satisfies the asymptotic behavior indicating that
model value exists.
with the resulting
value as 0. That is, if both the limits converge to zero the proposed model
satisfies the asymptotic behavior indicating that
model value exists.
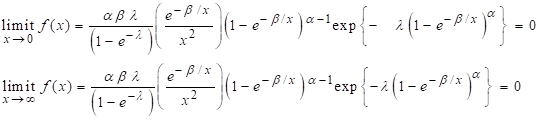 (6)
(6)
Since both the limits exist and have the limiting values
as zero, we confirm that the proposed modal has unique mode. The necessary and
sufficient conditions for mode are![]() and
and ![]() By using these
necessary and sufficient conditions, mode of the proposed model is obtained as,
By using these
necessary and sufficient conditions, mode of the proposed model is obtained as,
![]() (7)
(7)
2.8. Skewness
and Kurtosis
These are the measures that describe the nature like consistency of data and the normality of probability distribution. Bowley's skewness Al-Saiary et al. (2019) based on quartiles can be calculated using expression as
![]()
Moors (1988) and Al-Saiary et al. (2019) introduced kurtosis using Octiles given by the relation.
![]()
Q (.) is quantile functions of the model.
Statistical measures of this new model are obtained. For
this, 100 random samples from the quantile function mentioned in expression
(5). Here, we have taken initial values of the parameters as![]() . By using the generated values different basic statistics of
the proposed model are calculated. Table 1 Mean, Median, Mode, Sd, Skewness
and Kurtosis of IEEP
contains summaries for some set of parameters.
. By using the generated values different basic statistics of
the proposed model are calculated. Table 1 Mean, Median, Mode, Sd, Skewness
and Kurtosis of IEEP
contains summaries for some set of parameters.
Table 1
|
Table 1 Mean, Median, Mode, Sd, Skewness and Kurtosis of IEEP |
||||||||
|
α |
β |
λ |
Mean |
Median |
Mode |
Sd |
Skewness |
Kurtosis |
|
40 |
20 |
2 |
6.75 |
6.57 |
6.21 |
1.416 |
0.535 |
3.245 |
|
39.5 |
20 |
2 |
6.67 |
6.6 |
6.64 |
1.416 |
0.54 |
3.25 |
|
38.5 |
22 |
2 |
6.83 |
6.643 |
6.27 |
1.448 |
0.546 |
3.26 |
|
41 |
22 |
2 |
6.701 |
6.525 |
6.173 |
1.396 |
0.527 |
3.236 |
|
42 |
22 |
2 |
6.653 |
6.481 |
6.137 |
1.376 |
0.52 |
3.227 |
|
40.5 |
21.5 |
2 |
6.726 |
6.548 |
6.192 |
1.406 |
0.531 |
3.24 |
|
40 |
20 |
2 |
6.751 |
6.571 |
6.211 |
1.416 |
0.535 |
3.245 |
|
40 |
23 |
2.5 |
6.95 |
6.775 |
6.425 |
1.397 |
0.526 |
3.275 |
|
40 |
23 |
3 |
7.133 |
6.959 |
6.611 |
1.375 |
0.53 |
3.31 |
Standard deviation is decreasing when values of ![]() are increasing. Also values of
are increasing. Also values of ![]() are decreasing. Values
of skewness as well kurtosis is not unique showing that distribution is skewed
and not normal in nature.
are decreasing. Values
of skewness as well kurtosis is not unique showing that distribution is skewed
and not normal in nature.
2.9. Some Expansions
Following distribution is derived for studying the various
characteristic of the model by application of generalized binomial series.
Taking ![]() we can write.
we can write.
![]()
The power series expansion of corresponding to an exponential function is;
![]()
Using above two binomial series and exponential expansion in given pdf equation, the proposed model in series form is.
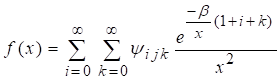 (8)
(8)
Where, 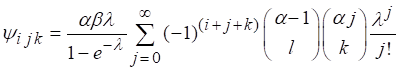
3. Calculation of moments
Quantitative measurements of the distribution in form of
function that describes characteristics of the probability distributions can be
explained using moments. The ![]() raw moment
raw moment ![]() new model
new model![]() is given as
is given as
![]() (9)
(9)
Integrating equation (9), we can get ![]() raw moments of the
IEEP can be obtained as
raw moments of the
IEEP can be obtained as
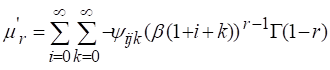
When r =1 then mean of the IEEP will be as
![]()
Second order raw moment of IEEP can be obtained taking r as 2. That is.
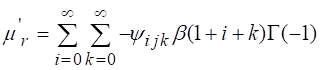
Using relation,![]() , variance can be obtained. Mean median and others measures
of the proposed model are given above in Table 1 Mean, Median, Mode, Sd, Skewness
and Kurtosis of IEEP.
Lower incomplete moments
, variance can be obtained. Mean median and others measures
of the proposed model are given above in Table 1 Mean, Median, Mode, Sd, Skewness
and Kurtosis of IEEP.
Lower incomplete moments ![]() is given by
is given by
![]() (10)
(10)
Lower incomplete gamma function ![]() and density functions are used to
and density functions are used to
find lower incomplete moment![]() as
as
![]()
The conditional moments is
![]() (11)
(11)
Upper incomplete gamma function is
![]()
Using density function and upper incomplete gamma function in equation (11), we can get conditional moment as.
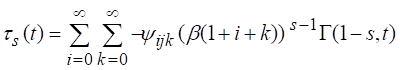
Similarly, MGF of the proposed model is given as;

Hence, we can get MGF as
![]() (12)
(12)
3.1. Residual Life Function
Here,![]() moment of the residual life of random variable X of the IEEP
can be defined by
moment of the residual life of random variable X of the IEEP
can be defined by
![]()
Expression ![]() can expanded using
binomial series expansions as,
can expanded using
binomial series expansions as,
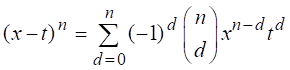
Hence, ![]() moment of residual
life of X of the distribution becomes.
moment of residual
life of X of the distribution becomes.
![]() (13)
(13)
Using upper incomplete gamma function in (13), we have
![]()
Also, ![]() moment of revised
residual life function of X of the proposed model IEEP is found as
moment of revised
residual life function of X of the proposed model IEEP is found as
![]()
Applying binomial expansion and substituting pdf, we can get following expression.
![]()
3.2. The probability Weighted
Moment
The probability weighted moment can be obtained using relation
![]() (14)
(14)
Applying the expansion of
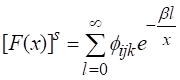 (15)
(15)
Where,
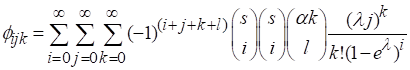
Now, using equations (14) and (15), we can write
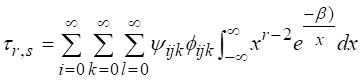 (16)
(16)
Integrating equation (17), we get
![]()
3.3. Order Statistics
Let ![]() is order statistics of
any sample of size n from IEEP. The PDF of
is order statistics of
any sample of size n from IEEP. The PDF of![]() order statistics David
& Nagaraja (2004) is defined as,
order statistics David
& Nagaraja (2004) is defined as,
![]() (17)
(17)
Where ![]() denotes the beta
function. Substituting the values of PDF and equation (16) replacing s by
denotes the beta
function. Substituting the values of PDF and equation (16) replacing s by![]() , we get
, we get
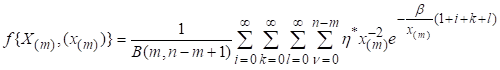 (18)
(18)
Where,
![]()
Now moment of the order statistics is
![]() (19)
(19)
Using equations (18) and (19) the ![]() moment of the order
statistics become
moment of the order
statistics become
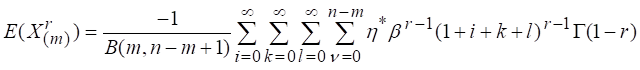
3.4. R'enyi and q-entropies
The entropy is used in many fields such as in statistics, mathematics, engineering, physics, thermodynamics etc. It can be used to measures the variation of uncertainty of the random variable R'enyi entropy is defined as;
![]() (20)
(20)
Applying the expansion of
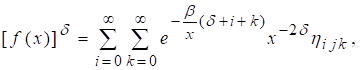 (21)
(21)
where, 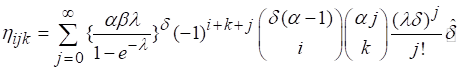
From equation (20), we can write
![]()
Similarly, we can define q-entropy as;
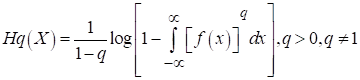
Thus, we can define the q-entropy is as.
![]()
4. Parameter Estimation Technique
4.1. Estimation using Maximum Likelihood
Here we found the MLE of the parameters for constructed
model. The MLE of the parameters are based on the observed sample x1,
x2,…,xn.
The likelihood function of parameters ![]() is given by
is given by
![]() (22)
(22)
Log likelihood function ![]() is given by
is given by
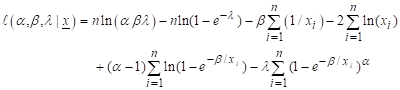 (23)
(23)
Here, differentiating the log likelihood function (23) and maximum likelihood estimators were obtained by equating the differentiated equations to zero. That is
![]() (24)
(24)
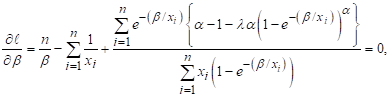 (25)
(25)
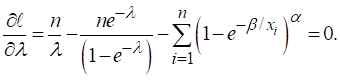 (26)
(26)
Estimation of unknown parameters![]() is done by solving nonlinear
equations (24), (25) and (26). It will be difficult in solving these equations
analytically so Newton- Rapson's iteration techniques is applied in log
likelihood function of equation (23) using
is done by solving nonlinear
equations (24), (25) and (26). It will be difficult in solving these equations
analytically so Newton- Rapson's iteration techniques is applied in log
likelihood function of equation (23) using ![]() function of R. Let
function of R. Let ![]() is MLE of
is MLE of ![]() Asymptotic normality
result is
Asymptotic normality
result is![]() . The fisher's information matrix
. The fisher's information matrix![]() given by;
given by;
![]() =
= 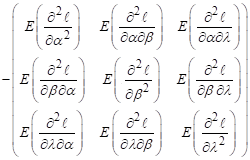
The maximum likelihood estimates (MLE) ![]() of
of ![]() was obtained by solving three nonlinear equations
analytically and using statistical software.
was obtained by solving three nonlinear equations
analytically and using statistical software.
The ![]() CI for constants
CI for constants ![]() and
and ![]() are obtained. Here we
have used asymptotic normality of MLE method and Variances of estimated
parameters using the inverse of
are obtained. Here we
have used asymptotic normality of MLE method and Variances of estimated
parameters using the inverse of ![]() of second derivatives of log
likelihood function. The second order derivatives are
of second derivatives of log
likelihood function. The second order derivatives are
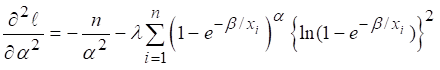
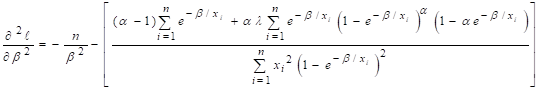
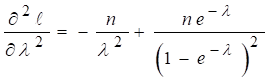
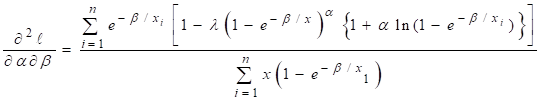
![]()
![]()
Let![]() is the parameter
vector and
is the parameter
vector and ![]() be corresponding MLE.
This provides (
be corresponding MLE.
This provides (![]() -
-![]() )
) ![]() N
N![]() (0, (
(0, (![]() )
)![]() ) as asymptotic normal
where
) as asymptotic normal
where![]() is fishers information
matrix given by
is fishers information
matrix given by
![]() =
=
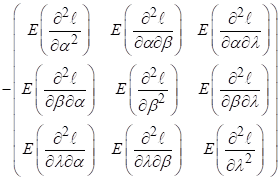
It will be worthless that MLE gives asymptotic variance![]() . Approximation of the
asymptotic variance can be done by taking estimated values of the parameters.
For this fisher’s information matrix
. Approximation of the
asymptotic variance can be done by taking estimated values of the parameters.
For this fisher’s information matrix ![]() which is given as;
which is given as;
![]() = -
= - 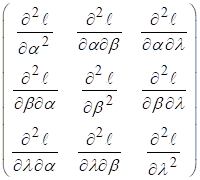 =
= ![]() where H is the
hessian.
where H is the
hessian.
We can obtain the observed information matrix maximizing the likelihood. For this Newton Rapshon algorithm is used. We have also find expression of variance covariance matrix as
![]() =
=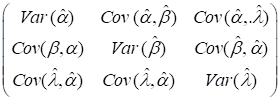
Hence from asymptotic normality of MLE approximate 100(1-![]() ) % CI for the
parameters are constructed using upper percentile
standard normal variate as,
) % CI for the
parameters are constructed using upper percentile
standard normal variate as,
![]()
where ![]() is the upper
percentile of standard normal variate.
is the upper
percentile of standard normal variate.
5. Applicability and data analysis
5.1. Data set
This section represents analysis of real dataset to verify the proposed model. Sometimes electro migration can occur in circuit because failures in microcircuit happen due to the movement of atoms in the circuits. Data is from an accelerated life test that includes 59 conductors Schafft et al. (1987); Nelson and Doganaksoy (1995) where failure time is measured in hours with no any censoring of the observations.
4.700, 6.545, 9.289, 7.543, 6.956, 6.492, 5.459, 8.120, 4.706, 8.687, 2.997, 8.591,6.129, 11.038, 5.381, 6.958, 4.288, 6.522, 4.137, 7.459, 7.495, 6.573, 6.538,5.589, 5.807, 6.725, 8.532, 9.663, 6.369, 7.024, 8.336, 9.218, 7.945,6.869, 6.352, 6.087, 6.948, 9.254, 5.009, 7.489, 7.398, 6.033, 10.092, 7.496, 7.974, 8.799, 7.683, 7.224, 7.365, 6.923, 5.640, 5.434, 7.937, 6.515, 6.476, 6.071, 10.491, 5.923 ,4.531.
5.2. Descriptive Data Analysis
Exploratory data analysis is a collection of different statistical analysis that explains and to summarize the data set used in research. Objective of this is to gain detailed idea of data set used. It may include some descriptive statistics as well as the graphical plots of the data. Following are main measures that can be included in descriptive data analysis.
· The boxplot, histogram, density curve etc. These are a graphical plot that help to find the pattern of the data and also helps to detect if there is any unusual pattern and observations in data.
· Measures of location, measures of scatters, skewness, and kurtosis etc gives some specific aspect and nature of the data.
R programming language is used to find summary of the data and the values obtained are tabulated below in table
Table 2
|
Table 2 Descriptive Statistics |
|||||||
|
Min. |
Q1 |
Q2 |
Mean |
Q3 |
Max. |
Skewness |
Kurtosis |
|
2.997 |
6.052 |
6.923 |
6.98 |
7.941 |
11.038 |
0.193 |
3.088 |
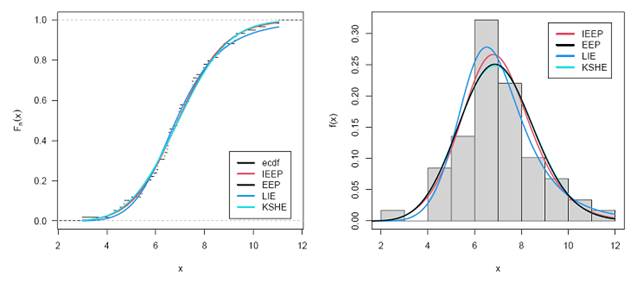
Figure 2 represents the boxplot and the histogram & and density fit of the proposed model IEEP.
Figure 2
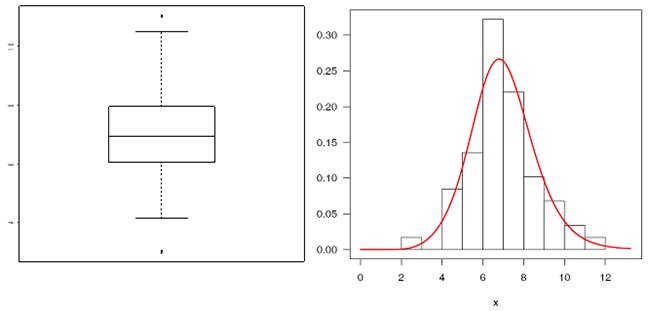
|
Figure 2 Boxplot (Left Panel) and Histogram and Fitted Density Plot (Right Panel) |
6. Parameter
estimation
There are various methods and tools for optimization of
the function. Forgetting maximum likelihood estimates (MLE) of the defined
model log-likelihood function defined in expression (23) is maximized. The
maximum likelihood estimates their standard error along with 95% confidence
Interval (CI) for parameters ![]() and
and![]() is obtained using R programming [R
Development core Team, (2016)]. We have also used the quasi-Newton-Raphson
algorithm in R [Rizzo, 2008] for maximum likelihood estimation.
is obtained using R programming [R
Development core Team, (2016)]. We have also used the quasi-Newton-Raphson
algorithm in R [Rizzo, 2008] for maximum likelihood estimation.
Table 3
|
Table 3 MLE, Standard Error and 95 Percent C. I |
|||
|
Parameters |
MLEs |
Standard
Error |
95%
C.l. |
|
alpha |
40.5868 |
4.86 |
(31.068, 50.113) |
|
beta |
22.7553 |
2.049 |
(18.739, 26.771) |
|
lambda |
2.9968 |
1.251 |
(0.5450, 5.4490) |
The profile plots of negative log-likelihood function of
proposed model for ![]() and
and ![]() are plotted separately and are shown in Figure 3.
are plotted separately and are shown in Figure 3.
Figure
3
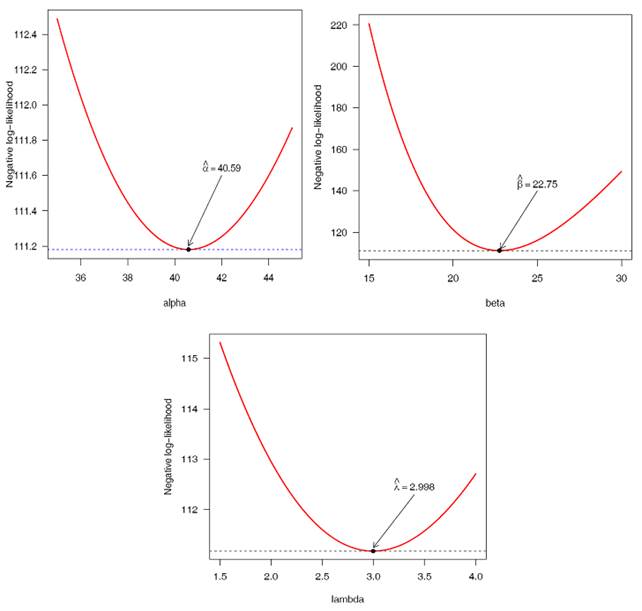
|
Figure 3 The Profile of
Negative Log-Likelihood Functions of |
Parameters and standard errors of IEEP and other models such as Exponentiated Exponential Poisson (EEP) Joshi (2017) Distribution, Logistic Inverse Exponential (LIE) Chaudhary and Kumar (2020), The Kumaraswamy Half-Cauchy distribution (KSHC) Ghosh (2014) distribution are estimated and are compared for the comparisons of the proposed model. Estimated parameters using MLE are mentioned in Table 4.
Table 4
|
Table 4 MLE and Standard Error of IEEP and the Other Distributions |
|||
|
Probability model |
|
|
|
|
IEEP |
40.5868(31.0160) |
22.7553(2.0490) |
2.9968(1.2510) |
|
EEP |
9.8700(4.5008) |
0.1774(0.0995) |
21.0934(27.1612) |
|
LIE |
5.3220(0.5830) |
- |
4.7357(0.1433) |
|
KSHC |
8.8568(5.7731) |
118.5980(119.7700) |
5.7472(4.9376) |
6.1. Model Comparison
Here, log-likelihood as well as the information criteria values like (i) Akaike's information criteria (AIC), (ii) Bayesian information criteria(BIC) (iii) Corrected Akaike's information criteria(CAIC), and (iv) Hannan-Quinn Information Criteria(HQIC)are calculated and tabulated in Table 2 and Table 5 Following relations are used to find the values of AIC, BIC, CAIC and HQIC.
![]() ,
,![]() ;
;
![]() and
and
![]() .
.
where n and k are total number of samples and total number of constants respectively. Since IEEP has least information criteria values with respect to the other competing, it is considered that IEEP fits data well.
Table 5
|
Table 5 AIC, BIC, CAIC and HQIC of IEEP and Other Models |
||||
|
Probability
model |
AIC |
BIC |
CAIC |
HQIC |
|
IEEP |
228.35 |
234.59 |
252.35 |
231.523 |
|
EEP |
228.65 |
234.88 |
252.65 |
231.813 |
|
LIE |
232.053 |
238.286 |
244.053 |
232.16 |
|
KSHC |
880.37 |
886.61 |
904.377 |
883.541 |
7. Model validation
For model validation, we can use different statistical
techniques. Here we have used two types of graphical plots; probability versus
probability (P-P) plots and quantile versus quantile (Q-Q) plots are drawn and
are shown in Figure 5. PP and QQ plots show
the theoretical distribution versus distribution. A P-P plot describes the
points; ![]()
![]() =
=![]() and
and ![]() is order statistics of
proposed model.
is order statistics of
proposed model. ![]() , is termed as the empirical distribution function, and
, is termed as the empirical distribution function, and ![]() is the indicator
function. In same way, the QQ plot
depicts the points;
is the indicator
function. In same way, the QQ plot
depicts the points;
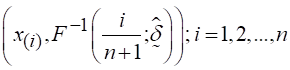 .
.
Figure 4
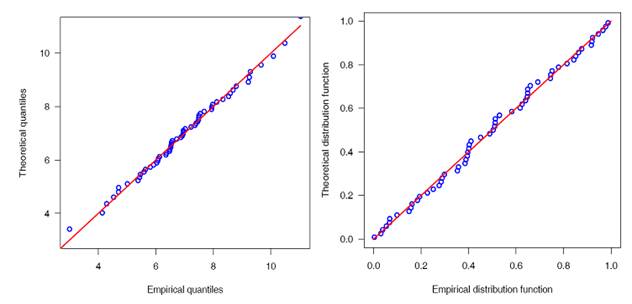
|
Figure 4 P-P Plot in Left Panel and Q-Q Plot in Right Panel of the IEEP |
The IEEP fits better in both the empirical and fitted case of distribution function. For model validation, Kolmogrov - Smirnov test showed D = 0.0520 with p-value = 0.9947 which means the model fits significantly. Curve for empirical distribution function and the fitted distribution function are plotted and is displayed in Figure 6
Total Time Test (TTT) plot is also shown in right panel of the Figure 6. The Empirical version of TTT plot is given as
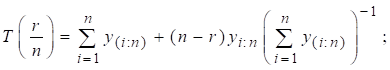
Where, r = 1, 2... n and ![]() be sample order statistics. Concave
shape of Curve of the TTT plot shows that hazard rate curve is increasing.
be sample order statistics. Concave
shape of Curve of the TTT plot shows that hazard rate curve is increasing.
Figure 5
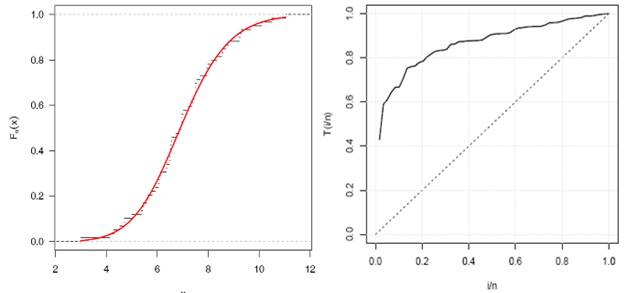
|
Figure 5 Theoretical Versus Empirical Plot (Left) and TTT Plot (Right) |
Figure 6 in left panel displays the empirical distribution curve and the fitted distribution curve for the newly defined model corresponding to other models. In Right panel of the Figure 6, histogram of the data and fitted density curve of the model under study and the competing models are displayed.
Figure 6
|
Figure 6 Estimated Fitted CDF with EDF (Left) and Estimated Fitted PDF |
8. Summary and Conclusion
This article is based on derivation, study and application of newly introduced probability model having three parameters. It is name as Inverse Exponentiated Exponential Poisson Inverse along with some statistical and mathematical properties, probability, weighted moments, order statistics, skewness, kurtosis, residual life time, entropy and survival functions etc. Different information criteria values are obtained for both the IEEP and the considering model and are compared. Study also showed that the goodness of fit statistics has least test statistics and higher p value respective to the other considering model. We have also plotted the empirical cdf versus the fitted cdf as well as the histogram versus the fitted density plot of the models. All the statistical computations and the graphical measures are performed using R language programming.
CONFLICT OF INTERESTS
None.
ACKNOWLEDGMENTS
None.
REFERENCES
Al-Saiary, Z. A., Bakoban, R. A., & Al-Zahrani, A. A. (2019). Characterizations of the Beta Kumaraswamy Exponential Distribution. Mathematics, 8(1), 23. https://doi.org/10.3390/math8010023.
Chaudhary, A. K., & Kumar, V. (2020). Half Logistic Exponential Extension Distribution with Properties and Applications. International Journal of Recent Technology and Engineering (IJRTE), 8(3), 506-512. https://doi.org/10.35940/ijrte.C4625.099320.
David, H. A., & Nagaraja, H. N. (2004). Order Statistics. John Wiley & Sons. https://doi.org/10.1002/0471667196.ess6023.
Ghosh, I. (2014). The Kumaraswamy-Half-Cauchy Distribution : Properties and Applications. J. Stat. Theory Appl., 13(2), 122-134. https://doi.org/10.2991/jsta.2014.13.2.3.
Gupta, R. D., & Kundu, D. (1999). Theory & Methods : Generalized Exponential Distributions. Australian & New Zealand Journal of Statistics, 41(2), 173-188. https://doi.org/10.1111/1467-842X.00072.
Joshi, R. K. (2017). The Analysis of Some Statistical Models. Doctoral Dissertation in Statistics Submitted to Deen Dayal Upadhyaya Gorakhpur University, Gorakhpur.
Kus, C. (2007). A New Lifetime Distribution. Computational Statistics & Data Analysis, 51, 4497-4509. https://doi.org/10.1016/j.csda.2006.07.017.
Marshall, A.W., & Olkin, I. (1997, September). A New Method for Adding a Parameter to a Family of Distributions with Application to The Exponential and Weibull Families. Biometrika, 84(3), 641-652. https://doi.org/10.1093/biomet/84.3.641.
Marshall, A. W., & Olkin, I. (2007). Life Distributions, 13.
Moors, J. (1988). A Quantile Alternative for Kurtosis. The Statistician, 37, 25-32. https://doi.org/10.2307/2348376.
Nelson, W., & Doganaksoy, N. (1995). Statistical Analysis of Life or Strength Data from Specimens of Various Sizes Using the Power-(Log) Normal Model. Recent Advances in Life-Testing and Reliability, 377-408. https://doi.org/10.1201/9781003418313-21.
Pham, H., & Lai, C. D. (2007). On Recent Generalizations of the Weibull Distribution. IEEE Transactions on Reliability, 56(3), 454-458. https://doi.org/10.1109/TR.2007.903352.
Rinne, H. (2009). The Weibull Distribution : A Handbook. CRC Press, Boca Raton. https://doi.org/10.1201/9781420087444.
Ristić, M. M., & Nadarajah, S. (2014). A new lifetime distribution. Journal of Statistical Computation and Simulation, 84(1), 135-150. https://doi.org/10.1080/00949655.2012.697163.
Schafft, H. A., Station, T. C., Mandel, J., & Shott, J. D. (1987 Feb 24). Reproducibility of Electro-Migration Measurements, IEEE Transactions on Electron Devices, ED-34, 673-681. https://doi.org/10.1109/T-ED.1987.22979.
 This work is licensed under a: Creative Commons Attribution 4.0 International License
This work is licensed under a: Creative Commons Attribution 4.0 International License
© Granthaalayah 2014-2023. All Rights Reserved.