Rethinking Chikku Kolam for Modern Adaptation. A study on Three Dimensional interpretations of the traditional art of Chikku Kolam

 

Hima Bindu Kondury ¹

 

¹ Assistant Professor, B. Des (ID), SPA, Jawaharlal Nehru Architecture and Fine Arts University, Hyderabad, Telangana

 

1. INTRODUCTION

As the human race evolved, man always drew inspiration from his natural surroundings to express himself. The earliest of mankind documented their surroundings in caves as paintings of animals and rituals giving a glimpse into his ability to observe and his need to express himself for the others to see as form of documentation. As man evolved, his ideas and scale of expressions also evolved gaining in grandeur like the petroglyphs seen in various ancient sites.

As times changed the nature worshipping man found various ways to highlight the various rituals giving rise to a very complex set of drawing forms. The Buddhist mandalas, the Sona sand drawings and the yantra and rangoli patterns are just a few of the unique patterns that have become an integral cultural aspect and hence have a profound cultural importance even in this modern world. It's interesting to note how some of these patterns have stood the test of time and find significance in various cultures across the globe and across millennia.  The Celtic Knot, the Swastika, Star of David are a few patterns that can be seen regularly in various cultures across various timelines. 

The Rangoli is one such practice that has stood the test of time and is practiced even to this day during various rituals and daily routine with much fervour. Known as Alpana in West Bengal, Aipan in Bihar, Mandana in Madhya Pradesh and Gujarat, these patterns are mostly inspired by the floral or nature patterns and follow the basic geometric principles of symmetry, radial design, emphasizing a focal point etc. 

The Chikku Kolam practiced predominantly in South Indian states of   Tamil Nadu and Andhra Pradesh developed very unique patterns which seem to have a complex mathematical understanding of grids, algorithms and predetermined parameters. It's interesting to draw parallels to various patterns that might exist in nature. This very thought is the basis for this research and as patterns in nature are rarely seen in just two dimensions the research is based on the thought that everything around has to be three dimensional thus occupying a certain space.

The method of study follows looking into similar patterns in the nature and some profound patterns formed by mathematical interpretations, geometry and its formulations of solid geometry, architectural built forms based on geometric interpretations, selection of an appropriate chikku kolam pattern for 3d exploration, various 3d models generated using the software “Blender “, 3d printing of some of the models that can find applications in real world

 

1.1. Dance of the planets and the patterns that they make

The ancient people of the Indian subcontinent spent a good amount of time observing the night sky and in turn the movement of the planets with reference to Mother Earth. A lot has been written and documented about the motion of the planets and its relevance in astronomy and astrology. It is indeed intriguing how the patterns formed by these planetary movements (dance of the planets) which globally came to be known as the Ptolemaic system in astronomy, is so similar to the chikku kolam. As a spiritual approach to chikku kolam, some researchers draw conclusion between the two wherein the “universe at the threshold” is applied at dawn as a spiritual protection to the household.

From the infinite space in the universe to the movement of electrons around the central nucleus in atoms, the pattern tends to follow the geometry of the chikku kolam, symmetry, radial expansion and an endless knot in which it is difficult to determine the starting and ending of the loop. The picture below gives the images or patterns formed by the movement of various planets with respect to Earth.

 

 

 

 

 

Figure 1

Figure 1 Patterns Formed by Revolution of Planets with Ref to Earth

 

1.2. Chladni plate sound vibrations and Lissajous curves.

Other interesting patterns that are created naturally and can be compared to chikku kolam are the sound patterns made by fine sand on Chladni plates. In an interview after her exhibition titled “Rangoli and Resonance Art”, art scholar Kumuda Krovvidi says “I have used sound frequencies to bring attention to universal patterns that correlate to those sound frequencies. These patterns are found in all of our surroundings, in snowflakes, in nautical shells, in animal life and plants in our Universe.” She further adds that what makes her study unique is the correlation of sound frequency patterns with chikku kolam. Chikku kolam patterns are usually created from a graph of dots that enable the geometry to remain intact and are amazingly like the meticulous records of patterns studied by physicists. Chaldni plates make it possible to visualize sound frequencies as patterns. The study of visual sound is called Cymatics and sound actually has a distinct geometry, much like crystals and flowers and nautilus shells. A striking similarity can be seen between these sound patterns and chikku kolam giving us an opportunity to look at these vibrations and behaviour of sound in a 3 dimensional format. (Sridhar).

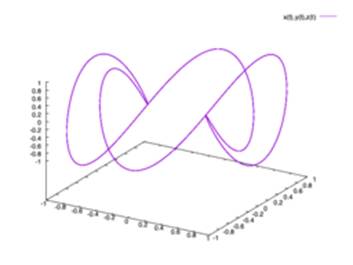
This concept can be further understood by the Lissajous curves. Lissajous curves or Bowditch curves can be described as an infinite number of curves that formed by intersecting of two simple sound oscillations that are perpendicular to each other i.e. the X and the Y planes. An intricate mesh like pattern is achieved when both the sound waves are of different frequencies which are very similar to the predetermined patterns of Chikku Kolam. Its interesting to note that when a third frequency is introduced to the Lissajous patterns, a very intricate three dimensional structures are formed. These three dimensional patterns are the basis for this study as the patterns formed are very similar to the chikku kolam patterns making one wonder if our ancestors had a deep knowledge of  the mathematical and scientific implications of sound waves in pattern formations and if they did it would be interesting to look at these chikku kolam as three dimensional forms. The picture below gives the correlating patterns of Chaldni plate sound vibrations and chikku kolam. The 3d image is of Lissajous curves of three varing sound waves that has been 3d printed.

Figure 2

 

Figure 2 Chaldni Plate Patterns

 

 Figure 3

Figure 3 Lissajous Pattern In 3D

 

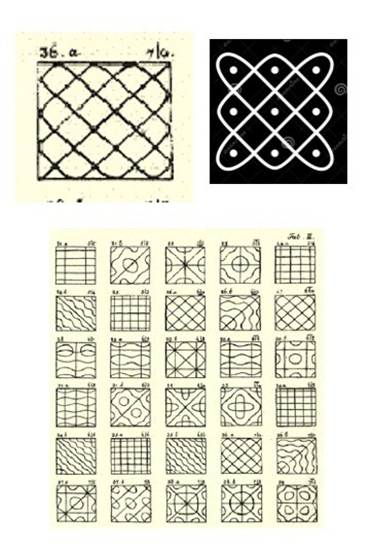
1.3. Understanding Geometry in Chikku Kolam

In their research paper “Fundamental Study on Design System of Kolam Pattern”, Yanagisawa and Nagata, talk of understanding the fundamental geometrical principles of Chikku Kolam from a morphological view point. They have managed to list out the various rules that are followed in making the kolam patterns and make use of computer aided calculations to determine the number of patterns that can be generated for a grid of predetermined parameters.

As per their computational generation, the various patterns that can be derived in a 1,7,1 grid and  the geometrical principles are listed as below

Total number of patterns 68,719,476,736

 Of them, One-strple 11,661,312 (0.017%) 

Of them, Unique 1,458,430 

Of them, Symmetrical 1,520 

1-axial 884 

180° rotational 612 

90° rotational 12 

2-axial + 180° rotational 12

Figure 4

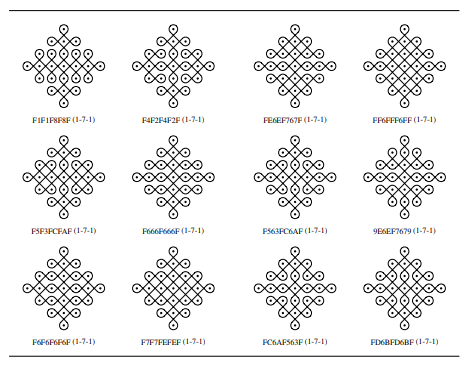
Figure 4 These are Symmetrical Patterns with Both Vertical and Horizontal Symmetry

 

Figure 5

Figure 5 These Patterns are Highly Symmetrical with 90 Degree Rotation

 

 Kolam patterns have such a clear and interesting design system, that countless various one-stroke patterns can be drawn following extremely simple elements and a few simple drawing rules. Large and complicated ones are also designed by joining small patterns based on a simple framework. These characteristic features of Kolam patterns have prospects to be applied to other areas, such as toy, puzzle game, tiling design, graphical language, architecture and city planning.

 

1.4. Understanding various methods of extruding 2d forms into 3d forms.

It's important to understand the progress that we have made in geometry and mathematics over ages and to understand the thoughts and methods that great thinkers have applied over years to actually understand how the 2d patterns can have a whole new meaning when explored in 3 dimensional space.

 

1.4.1.  Euclidean Geometry

Greek mathematician Euclid, in his book “Book of Elements” formulated the axioms and theorems for solid geometry which came to be known as Euclidian Geometry. Euclid spoke of formulae by which any regular polygon could be visualize as a three dimensional polyhedron depending on a set of axioms.  Regular polyhedra are the solid analogies to regular polygons in the plane. Regular polygons are defined as having equal (congruent) sides and angles. In analogy, a solid is called regular if its faces are congruent regular polygons and its polyhedral angles (angles at which the faces meet) are congruent. This concept has been generalized to higher-dimensional (coordinate) Euclidean spaces. Whereas in the plane there exist (in theory) infinitely many regular polygons, in three-dimensional space there exist exactly five regular polyhedra. These are known as the Platonic solids:

1)     the tetrahedron, or pyramid, with 4 triangular faces

2)     the cube, with 6 square faces

3)     the octahedron, with 8 equilateral triangular faces

4)     the dodecahedron, with 12 pentagonal faces

5)     the icosahedrons, with 20 equilateral triangular faces

Figure 6

Figure 6 Platonic Solids

 

With the development of various 3d modeling software a wide variety of three dimensional forms can be generated keeping intact the principles of Euclidean Geometry but with variable parameters. The picture shown below gives a idea of how a given dodecahedron can be designed into various different forms by varying the  parameters.

Figure 7

Figure 7 3D Adaptation of Platonic Solids

 

1.4.2.  Analytic Geometry in Three Dimensions

The Cartesian plane in Analytic Geometry is defined by two perpendicular number lines, the X-axis and Y-axis, which form the foundation for two-dimensional patterns. To locate a point in space, a third dimension, the Z-axis, is introduced, forming the basis of solid analytic geometry. Analytical Geometry combines algebra and geometry, representing geometric figures through algebraic equations in either a two-dimensional coordinate system or three-dimensional space. In a three-dimensional coordinate system, the X, Y, and Z axes define three planes: the XY plane, the XZ plane, and the YZ plane. These coordinate planes divide the space into eight octants, with the first octant containing all positive coordinates. Since Chikku kolam patterns have a well defined X and Y coordinates it’s interesting to see how these can be superimposed and studied in the third Z coordinate.

Source http://eagri.org/eagri50/MATH/lec01.html

 

 

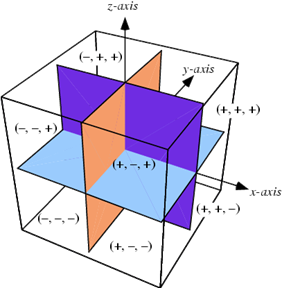
1.5. Geometry and Design

A branch of computational geometry known as geometrical design, deals with construction and representation of free form curves, surfaces or volume and is a precursor to geometric modeling. With the advancements of complex modeling software geometric modeling can be built for objects of any dimensions in any geometric space. Both 2D and 3D geometric models are extensively used in computer graphics, typology and technical drawings.

At the core of architectural design and research is architectural geometry which looks at design, analysis and manufacturing processes. With the use of these software architectural geometry can now explore various forms in contrast to the traditional forms and is being strongly influenced by various different fields such as differential geometry, topology, fractal geometry etc. To reach to a substantial understanding of these new forms it is necessary to look at some of the works of great thinkers, designers and artists who have put forward formulations for new and unique architectural designs.

 

 

1.5.1.  Geometry in Ancient Indian Temples

In her paper “Parametrizing Indian Kanata – Dravida Temples using Geometry”, author Sruti Goud gives a great understanding of the geometrical axioms applied in the complex temple designs of the Sanghmeshwara Temple emphasizing on the correlation between parametric extrusion of the temple design and ornamentation and the vastumandala principles for construction and ornamentation.

Figure 8

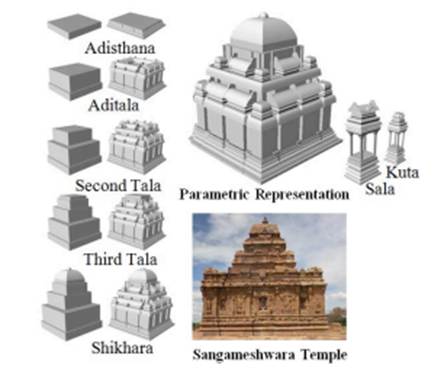
Figure 8 Parametric Understanding of Sanghmeshwara Temple

 

1.5.2.  Leonardo De Vinci - exploration in geometry

It becomes important to note how great artists have explored geometry to understand proportion and beauty. Leonardo De Vinci is the most noteworthy name that comes to mind when we speak of sacred geometry and his immense body of work gives us an insight to look into forms and their 3 dimensional development. Its uncanny to note when one follows the principles of geometry or the nature’s laws of harmony there seems to be a similarity to everything around and also to the Chikku Kolam.

The following figures talk of how computational and parametric thinking can be applied to De Vinci’s sketches of various churches to see how the process of design and 3d forms takes shape. Its interesting to note the similarity between the ancient temple architecture and the church design where the principles of extrusion and geometry remain the same.

Figure 9

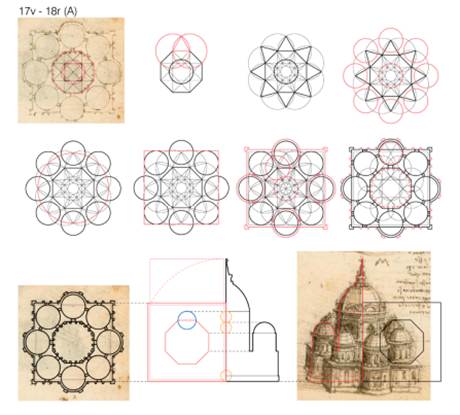
Figure 9 3D Extrusion of Churches Explored by Da Vinci in His Drawings

 

1.5.3.  Antonio Gaudi - Parametric Approach to built forms.

Antonio Gaudi and Frei Otto are the prominent designers in the realm of parametric design. Gaudi’s intricate catenary arches which he shaped by inverting the forms with upside – down models of churches and were the first in parametric design. He relied on analog computing – achieved this by suspending weighted strings and transforming the catenary arches by adjusting the positions of the weights. A mirror placed below reflected the model offering an intriguing design for the church.

Frei Otto experimented in parametric designs by employing form – finding activities derived from soap films and paths. He dabbled with free form structures using hanging models and water bubbles, expanding the design horizon with his experimental approaches.

Figure 10

Figure 10 Design Development Model of Sagrada Familia by Gaudi

 

Transitioning into the modern era, Zaha Hadid emerged as a potent force, propelling parametric design into the architectural mainstream. With audacious and futuristic designs, Hadid unleashed a new wave in architecture. Her architectural marvels such as the Guangzhou Opera House and the London Aquatics Centre reflected the transformative power of parametric design. Echoing dynamic flowing forms, these structures seamlessly blended within their settings, offering a distinctive visual appeal.

 

2. FINDINGS AND DISCUSSION   

Exploring 3 dimensional Chikku Kolam

Figure 11

Figure 11 Selected Chikku Kolam Pattern

 

The above kolam is the pattern selected for the exploration of 3d extrusions.

As seen in the study of the research the various patterns that can be derived in a 1,7,1 grid. The various patterns and the geometrical principles are listed as below

Total number of patterns 68,719,476,736

 of them, One-strple 11,661,312 (0.017%) 

of them, Unique 1,458,430 

of them, Symmetrical 1,520 

1-axial 884 

180° rotational 612 

90° rotational 12 

2-axial + 180° rotational 12

Though the possibility for a 1-7-1 grid chikku kolam is endless, the pattern selected serves as good example as it follows most of the geometric principles of a traditional chikku kolam 

·        It is formed by a continuous looped string which runs around the dotted grid to end at the starting point hence forming something known as the “Endless Knot”

·        The pattern is perfectly symmetrical on both the vertical axis and the horizontal axis.

·        The pattern could serve as a good case study as the loops that are formed cover a larger space in contrast to the loops quickly circling a single dot.

 

The following table gives the possible 3d extrusions that have been generated using various methods of 3d generation.

 

3. OBSERVATIONS

The three-dimensional exploration of the selected Chikku Kolam gave some interesting 3D forms that can find application in various fields such as product design, architecture, interior design, urban design etc. A detailed observation of various forms is listed below:

1)    Rounded and Modular Forms – The structure consists of multiple interconnected, cylindrical extrusions with smooth transitions, giving it an organic and natural aesthetic.

2)    Perforated Surface – The top surface features evenly spaced, rounded holes, suggesting a procedural or generative design approach.

3)    Uniform Height Variation – Unlike sharp or highly irregular extrusions, this one maintains a relatively consistent height, with soft undulations instead of dramatic peaks or spikes.

4)    Voxelized or Computational Approach – The design resembles patterns created using implicit modeling, metaballs, or cellular automata-based extrusions, often seen in architectural or computational design workflows.

This style is commonly employed in biomorphic architecture, generative design, and digital fabrication techniques like 3D printing or CNC milling.

The following images are those of 3D printed models using pla material.

 

The extrusion style used in the image appears to be variable-height or procedural extrusion, where the height of the extruded elements is determined by an underlying pattern or function. The structure follows these characteristics:

1)    Contour-Based Extrusion – The height of the vertical extrusions varies according to a predefined 2D shape or pattern, possibly a calligraphic or waveform-like design.

2)    Columnar or Cylindrical Segmentation – The extrusion is composed of multiple vertical segments, resembling cylinders or elongated prisms, rather than a continuous surface.

3)    Parametric or Algorithmic Approach – The smooth flow of curves and sharp spikes suggests the use of a procedural generation technique, often seen in parametric modeling or data-driven extrusion in 3D software like Blender, Grasshopper (Rhino), or Houdini.

This technique is commonly used in generative art, typography-based 3D modeling, and sound wave visualizations.

The following images are those of 3D printed models using pla material

 

 

 

The extrusion style in the above image appears to be a twisted, parametric, and faceted extrusion, characterized by:

1)    Helical or Twisting Motion – The structure features a dynamic, swirling form, suggesting a rotational extrusion technique where a base shape is extruded along a spiraling or twisting path.

2)    Faceted, Low-Poly Geometry – The surface has a sharp, angular, and polygonal appearance, indicating a low-resolution mesh or intentional faceting to enhance the sculptural quality.

3)    Procedural or Algorithmic Generation – The controlled yet complex form suggests the use of parametric modeling tools such as Grasshopper (Rhino), Houdini, or Blender’s modifiers (Twist, Subdivision, or Lattice Deform).

This extrusion technique is commonly used in generative architecture, 3D-printed sculptures, kinetic forms, and experimental computational design.

3D printing of this model was not feasible as the structure is complicated and the software used (Blender) was showing multiple errors for 3D printing.

 

 

The extrusion style in the above image appears to be contour-based organic extrusion with the following characteristics:

1)    Smooth but Faceted Surface – The model has an undulating yet polygonal surface, suggesting a low-resolution mesh extrusion or intentional faceting for a sculptural aesthetic.

2)    Vertical Growth with Variable Heights – Some sections extend further upwards than others, indicating a non-uniform extrusion height based on underlying contours or parametric control.

3)    Organic and Wave-like Deformation – The edges have a rounded, flowing curvature, likely influenced by a smooth procedural modifier like SubD or Laplacian Smoothing.

4)    Perforations and Cutouts – The presence of circular voids suggests an interplay between subtractive modeling (Boolean operations) and extruded forms.

This type of extrusion is commonly seen in computational design, 3D-printed architectural models, and organic parametric structures. It might have been created using tools like Grasshopper (Rhino), Blender, or Houdini, leveraging procedural height maps or contour-based extrusions.

The following images are those of 3D printed models using pla material

The model has been enhanced for the purpose of 3D printing as the software generated model seemed rough and unfinished. The extrusion principle has been retained.

 

The extrusion style in the above image appears to be modular, voxel-based extrusion with the following characteristics:

1)    Columnar Growth Structure – The extrusion extends vertically in a tree-like or mushroom-like formation, with clustered circular extrusions forming the "canopy" and elongated cylindrical extrusions forming the "trunks."

2)    Stacked, Step-Like Layers – The surfaces have a clear stepped or layered effect, indicating the use of contour-based height mapping or a low-resolution voxel-style extrusion.

3)    Hexagonal or Circular Module-Based Geometry – The extrusions are arranged in a repeating, geometric pattern, possibly influenced by cellular automata, parametric design, or a procedural growth algorithm.

4)    Bridge-Like Connection Between Structures – The connections between the three main extrusions suggest a generative algorithm that links modules dynamically, possibly simulating organic growth or branching.

3D printing for this model has not been explored due to the scale and intricacy of the design.

The extrusion style in the above image appears to be a parametric freeform lattice extrusion, featuring the following characteristics:

 

3.1. Key Features of the Extrusion Style

1)    Organic, Flowing Frame Structure

·        The framework consists of smooth, curved, and looping elements, suggesting a parametric algorithm was used to generate the shape.

·        The black structural frame follows fluid, freeform curves, giving it an organic, sculptural appearance.

2)    Surface-Based Extrusion with Wire Detailing

·        The inner mesh structure is made of thin, red curving wire-like lines, resembling a woven or networked pattern.

·        This suggests the use of secondary parametric elements to fill the primary structure.

3)    Asymmetric, Canopy-Like Form

·        The design lacks symmetry and appears to be inspired by tensile or pavilion-like structures.

·        The overall geometry is reminiscent of biomimicry-based architectural forms, such as tree canopies or insect wings.

 

 

4)    Supported by Vertical Columns

·        Unlike previous images, this structure is held up by vertical posts, indicating a partially suspended or pavilion-like function.

5)    Extrusion Techniques Used:

·        Profile Extrusion Along Curves:

1)     The thick black outlines suggest that curves were first drawn and then extruded along a path.

·        Surface-Based Meshing:

2)     The inner fine wire patterns were likely created using a Voronoi, network, or L-system growth algorithm.

The form looks like it was projected onto a non-planar surface, possibly with Rhino + Grasshopper, Houdini, or Blender Geometry Nodes.

3D printing of this structure was not executed because of the difficulty and failure of the structure.

The extrusion style in the above image appears to be organic, curvilinear parametric extrusion with the following characteristics:

 

3.2. Key Features of the Extrusion Style:

1)    Ribbon-Like Structural Extrusions – The dominant form consists of thick, looping curves that appear to be tubular splines or NURBS-based extrusions, following a fluid, interconnected pattern.

2)    Wireframe-Like Inner Structure – The interior contains a finer network of thin, chaotic wire-like elements, possibly generated using a particle-based growth algorithm or randomized curve extrusions.

3)    Dome-Like Overall Form – The general shape suggests an arching, semi-spherical structure, often seen in biomorphic architecture, tensile structures, or procedural parametric designs.

The following images are those of 3D printed models using pla material

The framework like inner membrane was difficult to 3D print. The structure has also been modified by printing only the above half as the dome like structure would find appropriate function in real world scenario. Any light fabric like covering would go perfectly with the structure.

As this dome like form serves the purpose of a structure to cover a certain space and yet keeping in mind the aesthetical and cultural importance of Chikku Kolam, the method of the extrusion has been considered for further study. A more complex Chikku Kolam pattern has also been explored in a similar fashion image of which have been shares below:

The above images are 3D models generated using the software Blender.

The 3D printed models of the same are as below:

 

The following study of 3D extrusions gives us an idea of creating a module of a 3D form that can be replicated as per the requirement to cover a certain area, a structure that can be employed to cover various pockets of space such as public spaces in urbanscapes, exhibition spaces etc.

 

4. Conclusion

The art of Chikku Kolam is of great significance in the South Indian states of Tamil Nadu, Andhra Pradesh and Telangana. It is indeed mesmerizing to note how these complex geometric patterns that follow various principles of geometry are meticulously recorded and handed down since generations by the women and the young girls of the household. This knowledge of generating such complex patterns is slowly vanishing from the busy urbanized cities and does require efforts to be conserved and protected and also find newer ways of finding relevance in the urbanized cities. Blending technology and tradition together is the way ahead to foray in terms of design and architecture.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

I would like to thank my student, Saifuddin Khwaja for his immense support in generating the 3D models and also in 3D printing of the same. I also take this opportunity to thank my student, Meghnath Naidu for his help with the 3D model generation. This paper is part of the research grant provided by the University, SPA, Jawaharlal Nehru Architecture and Fine Arts University, Hyderabad. I would also like to mention the use of Meta AI for streamlining the thought process for this paper.

 

REFERENCES

Britannica. (2024). Knot Theory | Mathematics & Topology. Retrieved 2024, September 18.

Illustrarch. (n.d.). What is Parametric Architecture and Who are the Pioneers?

Nagata, S., & Yanagisawa, K. (2007). Fundamental Study on Design System of Kolam Pattern.

Goud, S. (n.d.). Parametrizing Indian Karnata-Dravida Temple Using Geometry.

Sengupta, S. (2019). Kolam Traditions in South India. DK Printworld.

Shankar, A. K. (2016). Pulli Kolam and the Creative Mind. Palaniappa Brothers.

Sridhar, A. (2023, October 3). The Cosmic Art of Rangoli Designs and Sound Vibrations. Center for Soft Power. Retrieved 2024, September 17.  

Star in the Stone. (n.d.). Ernst Haeckel.

Storm Math. (n.d.). Precalculus - Chapter 11.

Vaienti, B., Apollonio, F. I., & Gaiani, M. (2020). Analysis of Leonardo da Vinci’s Architecture through Parametric Modeling: A Method for the Digital Reconstruction of the Centrally Planned Churches Depicted in Ms. B. Heritage, 3(4), 1124-1147. https://doi.org/10.3390/heritage3040063

Wikipedia. (2024, December 1). Geometric Design.

Wikipedia. (n.d.). Geometric Design. Retrieved 2024, December 1.

Wikipedia. (n.d.). Lissajous Curve. Wikipedia, The Free Encyclopedia.

Yangchenma Arts & Music. (2020, July 9). Sacred Geometry Course: Dance of the Planets. Retrieved 2024, September 29.