Novel Way of Determining Sum of k^th powers of Natural numbers

 

V.R. Kalyan Kumar ¹, Dr. R. Sivaraman ²

 

¹ Independent Research Scholar, California Public University, USA

² Associate Professor, Post Graduate and Research Department of Mathematics, Dwaraka Doss Goverdhan Doss Vaishnav College, Arumbakkam, Chennai, India

 

1. INTRODUCTION

1.1.    Definition

Let us denote the sum of k^th powers of first n natural numbers by

 

                                                                                                      (1)

 

We notice that,

 

 

1.2. Differentiation of  for k ≥ 0

In view of formulas presented in Senthil et al. (2014) , we know that  is a polynomial in n of degree k + 1. Hence  is differentiable for each k ≥ 0. We now differentiate  for few values of k to notice some pattern.  

 

For k = 0, we know that

 

Hence,  (                                                                                                            (2)

 

Now, for k = 1, =  n² +   n

 

Differentiating and simplifying we get

 

( n +    =                                                                                                      (3)

 

For k = 2,  n +    n² +   n³ 

 

Differentiating and simplifying we get

 

(   + n + n² =                                                                                          (4)

 

For k = 3,  n²   n³   n⁴

 

Differentiating and simplifying we get

 

(   n   n²  n³  = 3                                                                         (5)

 

For k = 4,   n n³  n⁴   n⁵

 

Differentiating and simplifying we get

 

( n²n³n⁴  = 4                                                   (6)

 

By observing equations from (3) to (6), we could see that differential of sum of k^th powers of natural numbers is equal to k times sum of (k–1)^th powers of natural numbers plus a constant. But what are those constants? To see this, we make the following definition.

 

 

 

1.3. Definition of Bernoulli Numbers

Bernoulli Numbers are numbers which occur as coefficients of  in the Taylor’s series expansion of  about x = 0. We denote the nth Bernoulli Number by . For knowing more about Bernoulli numbers and their properties see Sivaraman (2020)   

 

Thus, by definition we get                                                                 (7)

 

We notice that the constant term of  is 1 and so we obtain.

 

In view of Sivaraman (2020), we know that the Bernoulli numbers satisfy the equation

 

                                                                                                                 (8)

 

Using the fact that B₀ = 1 and (8), the first few Bernoulli numbers are given by

 

  

 

1.4. Construction of Faulhaber’s Triangle        

We now construct a triangle of numbers whose entries are denoted by T(p,q) where q = 0,1,2,3,…,p. Here p denote the row beginning from 0 and q denote the column beginning with 0 and ending with p for given value of  p.  The entry of row 0 should be 1. That is, T(0,0) = 1. Assuming that row p – 1 is known, the entries in the pth row is given by the formula

 

 

Equation (10) is used to compute T(p,1) up to T(p,p).

The entries in the p^th row, first column is calculated in such a way that the row sum is always 1. That is, we should have

 

 

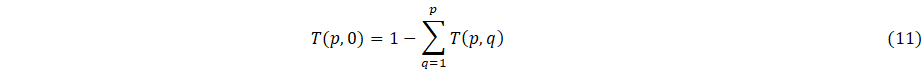
Equations (10) and (11) are used to construct the following triangle up to first eleven rows. 

Figure 1

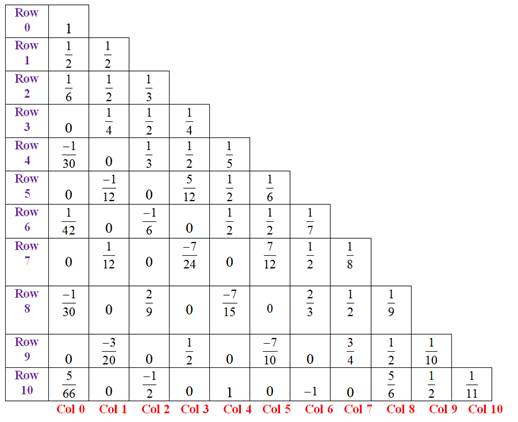
Figure 1 Faulhaber Triangle

 

From (9) and column 0 of Figure 1, we notice that T(k,0) = B_k, where B_k is the k^th Bernoulli number.  For knowing more about Faulhaber’s Triangle and its entries see Sivaraman (2020).

 

Generalizing equations (3) to (6), I now prove the following important theorem.

 

1.5. Theorem 1

If  is sum of k^th powers of natural numbers, then

 

 (                                                                                                (12)

 

where B_k is the k^th Bernoulli number. 

 

Proof: In view of Faulhaber’s Formula presented in Sivaraman (2020), we notice that

 

 =  +  +  + + +...++                                       (13)

 

Differentiating the expression on both sides of (13) and simplifying we get

 

(+++   +

 

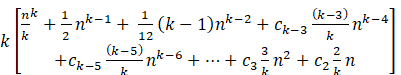=  +(14)

 

But from (13), we notice that

 

 

   =   +  +  + + + … + +                            (15)

 

We now notice that the coefficients in  and in terms of entries of Faulhaber’s Triangle are given by

 

 

Now using (10), (16) and (17), we deduce the following

 

 

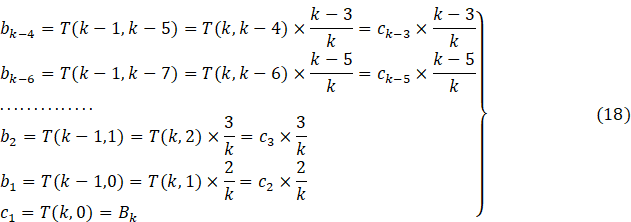
Substituting (15) and (18) in (14), we get

 

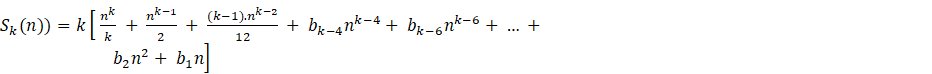( + B_k

Hence, we obtain (

 

This completes the proof.

 

2. Conclusion

In this paper, using the concepts of Bernoulli numbers and Faulhaber’s Triangle, we have provided a novel method by proving a theorem that the derivative of sum of k^th powers of first n natural numbers is k times the sum of (k – 1)^th powers of first n natural numbers plus the k^th Bernoulli number. This differential recurrence relation between successive powers of sum of first n natural numbers is very important in the sense that it helps us to obtain  knowing  and Bernoulli numbers.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Dinesh, A., & Sivaraman, R. (2022). Asymptotic Behavior of Limiting Ratios of Generalized Recurrence Relations, Journal of Algebraic Statistics, 13(2), 11-19.

Sivaraman, R. (2020). Summing Through Integrals, Science Technology and Development, 9(4), 267-272.

Senthil, P., Abirami, R., & Dinesh, A. (2014). Fuzzy Model for the Effect of rhIL6 Infusion on Growth Hormone, International Conference on Advances in Applied Probability, Graph Theory and Fuzzy Mathematics, 252, 246.

Senthil, P., Dinesh, A., & Vasuki, M. (2014). Stochastic Model to Find the Effect of Gallbladder Contraction Result Using Uniform Distribution, Arya Bhatta Journal of Mathematics and Informatics, 6(2), 323-328.

Sivaraman, R. (2020). Bernoulli Polynomials and Faulhaber Triangle. Strad Research, 7(8), 186-194. https://doi.org/10.37896/sr7.8/018.

Sivaraman, R. (2020). Remembering Ramanujan, Advances in Mathematics: Scientific Journal, (Scopus Indexed Journal), 9(1), 489-506. https://doi.org/10.37418/amsj.9.1.38.

Sivaraman, R. (2020). Sum of Powers of Natural Numbers, AUT AUT Research Journal, 11(4), 353-359.

Sivaraman, R. (2020). Summing Through Triangle, International Journal of Mechanical and Production Engineering Research and Development, 10(3), 3073-3080. https://doi.org/10.24247/ijmperdjun2020291.

Sivaraman, R. (2021). Recognizing Ramanujan's House Number Puzzle, German International Journal of Modern Science, 22, 25-27.

Sivaraman, R. (2021). Pythagorean Triples and Generalized Recursive Sequences, Mathematical Sciences International Research Journal, 10(2), 1-5.

Sivaraman, R., Suganthi, J., Dinesh, A., Vijayakumar, P. N., & Sengothai, R. (2022). On Solving an Amusing Puzzle, Specialusis Ugdymas/Special Education, 1(43), 643-647.