Granthaalayah

q-SPACE (q-TIME)-DEFORMATION OF THE CONTINUITY EQUATION

 

Hakeem A. Othman 1Icon Description automatically generated

 

1 Department of Mathematics, AL-Qunfudhah University College, Umm Al-Qura University, KSA

1 Department of Mathematics, Rada'a College of Education and Science, Albaidha University, Albaidha, Yemen

 

A picture containing logo Description automatically generated

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Received 6 August 2021

Accepted 19 August2021

Published 31 August 2021

Corresponding Author

Hakeem A. Othman, hakim_albdoie@yahoo.com

DOI 10.29121/granthaalayah.v9.i8.2021.4177

Funding: This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Copyright: © 2021 The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

 

 

 

 

ABSTRACT

 

A q-space (q-time)-deformation of the continuity equations are introduced using the q- derivative (or Jackson derivative). By quantum calculus, we solve such equations. The free cases are discussed separately.

 

Keywords: q-Derivative, q- Space Deformation Continuity Equation, q-Time Deformation Continuity Equation, q-Calculus

 

1.    INTRODUCTION

         Generally speaking, Continuity equations can comprise both "source" and "sink" items, which permit them to give an account of amounts that are almost preserved, such as the density of sorts of molecules which can be produced or demolished by chemical interactions.

That is to say Continuity equations underlie more specific transfer equations like Navier–Stokes equations, Boltzmann transport equation, and the convection spread equation.

By the diversity theory, a comprehensive continuity equation can also be shaped in a” variant form”:

 

         σ is the generation of Q per unit volume per unit time, it is time; j is the flux of Q, ρ is the amount of the quantity Q per unit volume where ∇ is divergence

When Q is a preserved quantity that cannot be formed or ruined (such as energy), σ = 0 and the equations become:

 

 

         In the field of Mathematics, a q-analog of a theory, sameness or manifestation is an act of generalizing, counting another parameter q that returns the original theory, expression in the limit as q → 1. Mathematicians are, typically, interested in q-analogs that rise naturally, rather than in randomly devising q-analogs of known results. The earliest q-analog dealt with in detail is the basic hyper geometric series, which was presented in the 19th century.

 

 

In this way, it is normal to ask what is the q-Space (q-time)-deformation of the continuity equation.

The present paper has been arranged as follows:

Section 1 introduces the topic theory. Section 2 briefly will give an exposition of some basic concept and preliminaries of the language of q-calculus. In section 3, we introduced free q-Space (free q-time)-continuity equation, and we deduced some theorems. Finally, in Section 4, we study q-Space (q-time)-deformation of the continuity equation.

In future works, we will try to extend the continuity equation in the quantum white noise setting, see [8 and 9]

 

2.    PRELIMINARIES

We will give an exposition of some basic concept and preliminaries of the language of q-calculus (see [1, 2, 3, 4, 5, 6, and 7]). Therefore, natural number n has the following q deformation:

 

 with

 

Sporadically we will write [∞] q for the limit of these numbers: 1/((1-q)). The q factorials and q binomial coeffcients are defined naturally as

 

 with

 

For q ∈ (0,1) and analytic f:C⟶C define operators Z and D_ (q) as follows:

 

 

                  

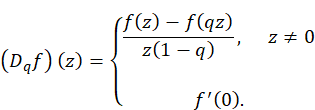
The probability distribution of a non-commutative random variable , where a is a bounded operator on some Hilbert space satisfying, the distribution probability of a non-commutative arbitrary changeable ,

 

 for some                                                              (1)

 

 

3.    FREE-SPACE (FREE-TIME)-CONTINUITY EQUATION

In this section, the free-Space (Free-Time)-continuity equation cases are discussed.

 

3.1.  FREE-SPACE-CONTINUITY EQUATION

Let Dt   given by

 

                                                        (2)

 

As a free analogue of the continuity equation

we will study the following equation

 

                                                                                                                       (3)

 

Theorem 1: The free-space-continuity equation (3) gives

 

 

Where  and  are given.

Proof: Using (2) in equation (3), we get

 

                                                                                           (4)

 

Then

 

 

Therefore, we obtain

Which complete the proof.

 

3.2.  FREE-TIME-CONTINUITY EQUATION

Let Dt given by

 

 .                                                               (5)

 

As a free analogue of the continuity equation

 

 

we will study the following equation

 

                                                                                                                      (6)                                                                                                     

 

Theorem 2. The free-time-continuity equation (6) gives

 

,

 

where  and  are given.

 

Proof:  Using (5) in equation (6), we get

 

And then

 

 

Therefore, we obtain

 

which completes the proof

 

 

4.    q-SPACE-DEFORMATION OF THE CONTINUITY EQUATION

Let q∈ (0,1), Recall that

 

                                                                                             (7)

 

As a q-space-deformation of the continuity equation

 

 

we will study the following equation

 

                                                                                                                    (8)

 

Theorem 3:  For q∈ (0,1), the q-space-deformation of the continuity equation (8) gives

 

 

Where  and  are given.

Proof: From equation (7), we get

 

                                                                                            (9)

 

And, then

                                                           ∙

                                                           ∙

                                                           ∙

.

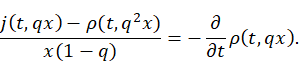
Then, we obtain

                                                                  ∙

                                                                  ∙

                                                                  ∙

.

 

Therefore, we deduce that

 

 

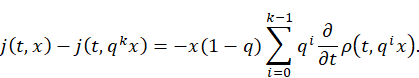
As  k→∞, we get

 

 

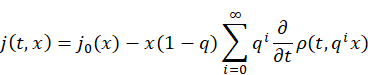
which completes the proof.

 

5.    q-TIME-DEFORMATION OF THE CONTINUITY EQUATION

Let q∈ (0,1). Recall that

 

                                                                                  (10)

 

as a q-time-deformation of the continuity equation

 

 

we will study the following equation

 

                                                                                                                 (11)

 

 

Theorem 4. For q∈ (0,1), the q -time-deformation of the continuity equation (2) gives

 

 

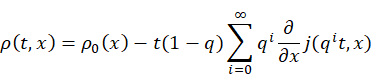
Where  and  are given.

Proof:  From equation (10), we get

 

                                                                                 (12)

 

And, then

                     

                                                 ∙

                                                 ∙

                                                 ∙

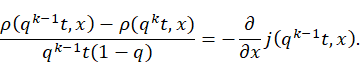
Then, we obtain

                                                                   ∙

                                                                   ∙

                                                                   ∙

Therefore, we deduce that

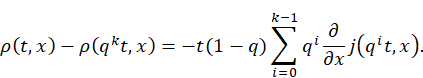
As  k→∞, we get

 

 

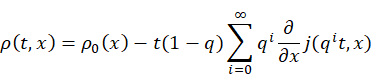
which complete the proof.

 

REFERENCES

C. R. Adams, On the linear ordinary q-difference equation, Am. Math. Ser., II, 30, pp. 195-205, (1929). Retrived from https://doi.org/10.2307/1968274

G. Bangerezako, Varitional q-calculus, J. Math. Anal. Appl., 289, pp. 650-665, (2004). Retrived from https://doi.org/10.1016/j.jmaa.2003.09.004

H. F. Jackson, q-Difference equations, Am. J. Math., 32, pp. 305-314, (1910). Retrived from https://doi.org/10.2307/2370183

H. Rguigui, Characterization of the QWN-conservation operator, Chaos, Solitons & Fractals, Volume 84, 41-48, (2016). Retrived from https://doi.org/10.1016/j.chaos.2015.12.023

H. Rguigui, Wick Differential and Poisson Equations Associated to The QWN-Euler Operator Acting On Generalized Operators, Mathematica Slo., 66 (2016), No. 6, 1487-1500. Retrived from https://doi.org/10.1515/ms-2016-0238

Hakeem A. Othman," The q-Gamma White Noise", Tatra Mountains

Mathematical Publications, 66 (2016), 81 – 90.  Retrived from https://doi.org/10.1515/tmmp-2016-0022

S. H. Altoum., H. A. Othman, H. Rguigui, Quantum white noise Gaussian kernel operators, Chaos, Solitons & Fractals, 104 (2017), 468-476. Retrived from https://doi.org/10.1016/j.chaos.2017.08.039

Sami H. Altoum, q deformation of Transonic Gas Equation, Journal of Mathematics and Statistics, 14(2018),88-93. Retrived from https://doi.org/10.3844/jmssp.2018.88.93

W. H. Abdi, On certain q-difference equations and q-Laplace transforms, Proc. Nat. Inst. Sci. India Acad , 28 A, pp. 1-15, (1962).

 

 

Creative Commons Licence This work is licensed under a: Creative Commons Attribution 4.0 International License

© Granthaalayah 2014-2021. All Rights Reserved.