introduction of single stage trade credit policy in the inventory system. Huang (2003) extended the concept between supplier and retailer. He assumed that retailer’s offered credit period to the customer is less than the credit period offered by the supplier to the retailer. Jaggi et al. (2008) introduced credit linked demand rate in their model. Chung (2013) implemented the concept of two-level trade credit periods in economic production quantity model with storage capacity constraints. Chung et al. (2014) considered the facility of permissible delay in payment in economic production quantity model for deteriorating items. Giri and Sharma (2016) incorporated the concept of permissible delay in payment in a model where demand rate increases linearly with time. Pal (2018) examined the effect of trade credit policy with partial backlogging of shortages. Giri and Sharma (2019) developed inventory model with partial trade credit policy. Tiwary et al. (2018) introduced two level partial trade credit policy in a three-echelon supply chain associated with perishable items. Mandal et al. (2020) introduces reliability in a production inventory model with two tier credit policy. An inventory model with two stage deterioration under the atmosphere of permissible delay option was formulated by Pal et al. (2021).

 

2.    NOTATIONS

Q	Ordering quantity of the retailer
W	Purchasing cost per unit item of the retailer
P	Selling price per unit item of the retailer
S	Set up cost
D	Demand rate
	Holding cost per unit item
	Cycle length
	Credit period offered by the bank to the retailer
	Credit period offered by retailer to the customer
	Obtained interest rate
	Paid interest rate.
	A fraction portion of the total customer make immediate payment on purchase of goods
	Retailer’s inventory level at time

 

3.    BASIC ASSUMPTIONS

·        A single item is considered

·        Time horizon is infinite

·        Retailer has some capital to arrange set-up cost. But he has to go for bank loan for ordering quantity . Banks provide a credit period. After that period bank will charge interest for remaining unpaid amount. Retailer can enjoy interest from sells revenue up to the time .

·        Obtained interest rate is less than paid interest rate.

·        Retailer faces two types of customers. One category wants to pay immediately after purchase of a thing while another category wants to avail some time delay for making payment.

·      Retailer offers a credit period  to the customer and sells all items by the time. From the point of category of customer enjoying permissible delay in payment scheme, if buys item at time  arranges payment at time .

·        Retailer’s offered credit period is less than his cycle length

·      Demand rate  is a monotonic function which decreases linearly with selling price .  Exact form of demand rate is   with .

 

4.    MODEL FORMULATION WITH JUSTIFICATION

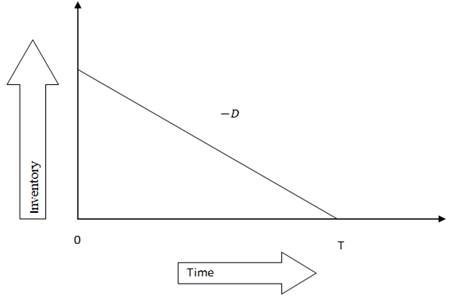
Figure 1 Retailer’s time weighted inventory

 

Retailer ordering quantity is .  This amount depletes at the rate .

The differential equation which governs inventory level of the retailer is given below.

 

 subject to initial condition                                                                         (1)

 

Solution is given by

 

                                                                                                                (2)

 

Terminal condition   gives,                                                                   (3)

 

Total holding cost is given as

 

 =   [ using (2) and (3)]                                                                  (4)

 

Retailer goes for bank loan for purchasing amount . So, bank loan amount is

. Two cases come up.

Either Case1.  or Case2. . Now, Case 2 can be subdivided into three Sub Cases on the basis of the fact that retailer collects his final payment from the customer at time . Possible three Sub Cases are given below.

Sub Case2.1
        Sub Case2.2

Sub Case 2.3

 Now we will discuss all situations with figures.

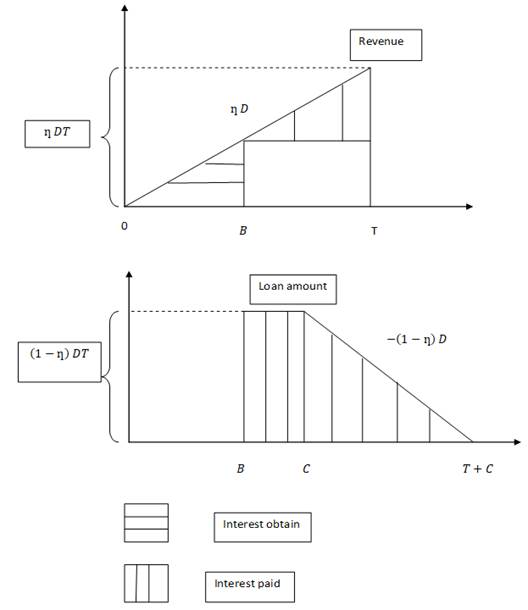
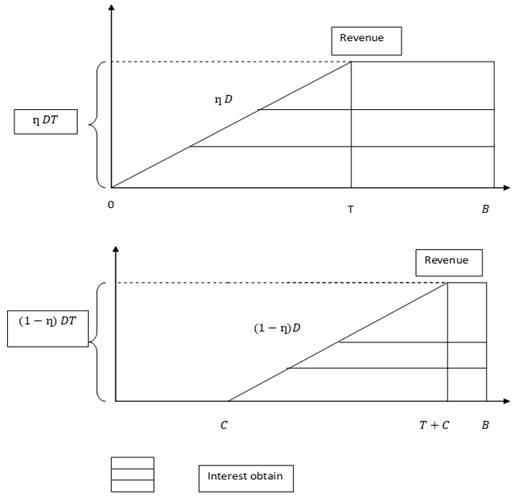
 Case 1.

Figure 2 Immediate payment scheme (above) and trade credit situation (below) under Case 1

 

For immediate payment, retailer enjoys the interest from sales revenue for the period  . He has to pay interest for the period .

Interest obtained =  , Interest paid =

For permissible delay in payment scheme, retailer does not enjoy any interest from sales revenue. Interest paid =  

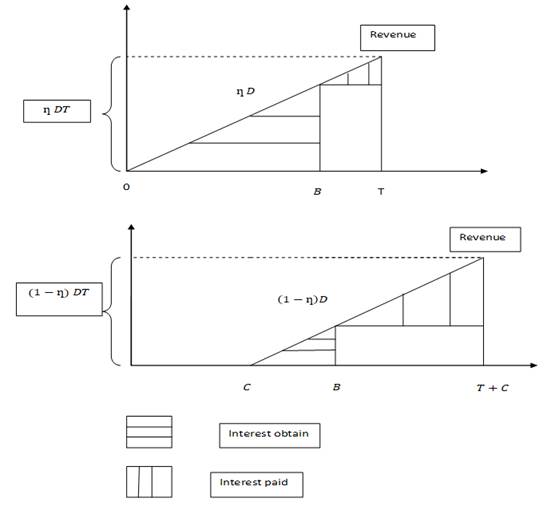
Case 2.1:

 

Figure 3 Immediate payment scheme (above) and trade credit situation (below) under Sub Case 2.1

 

For immediate payment, Interest obtained =  , Interest paid = .

For permissible delay in payment scheme,

Interest obtained =  ,

Interest paid =

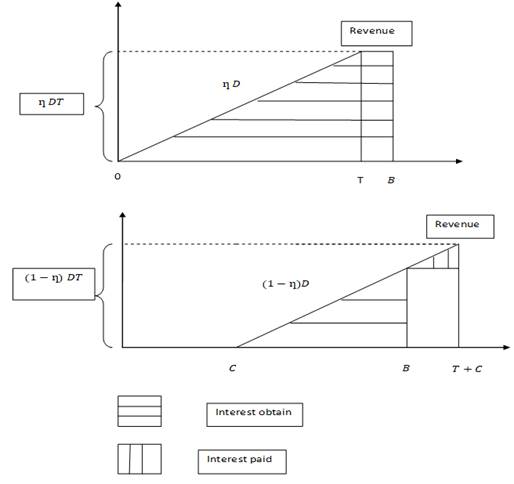
Case 2.2:

 

 

 

 

 

 

 

 

 

 

Figure 4 Immediate payment scheme (above) and trade credit situation (below) under Sub Case 2.2

 

For immediate payment, Interest obtained =  

Interest paid = 0.

For permissible delay in payment scheme,

Interest obtained =  

Interest paid =

Case 2.3:

Figure 5 Immediate payment scheme (above) and trade credit situation (below) under Sub Case 2.3

 

Interest obtained =  

Interest paid = 0

For permissible delay in payment scheme,

Interest obtained =  

Interest paid = 0

Retailer’s average profit = (Selling price – Bank loan- Set up cost- Holding cost + Interest obtained from sales revenue –Interest paid to the bank) / Cycle length.

Average profit function of the retailer for different situations is given in the following table.

Table 1
Case / Sub Case	Profit function	Expression
1
2.1		[ + ] / T
2.2		[ + +  ] / T
2.3

 

5.    SOLUTION METHODOLOGY

We first solve the following partial differential equations

 

 

 

Then we get solutions for cycle length and selling price as  . These solutions are optimal if the eigen values of the following Hessian matrix at  are negative.

 

 

 

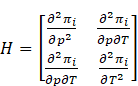
6.    NUMERICAL EXAMPLE

Values of parameters for different situations are given below.

Common parameters to all situations.

	$500 per set up
	$1.5 per unit
	$0.07 per annum
	$0.09 per annum
	0.3
	$6 per unit
	100
	4

 

Parameter varies along with situations.

Case 1	Sub Case 2.1	Sub Case 2.2	Sub Case 2.3

 

Optimal results obtained

	Case 1	Sub Case 2.1	Sub Case 2.2	Sub Case 2.3
	$17.56	$17.11	$16.58	$15.99
	4.01	3.86	3.54	3.25
Average profit	$99.07	$124.10	$163.01	$238.36

Conditions of optimality

Eigen values of the hessian matrix	Case 1	Sub Case 2.1	Sub Case 2.2	Sub Case 2.3

 

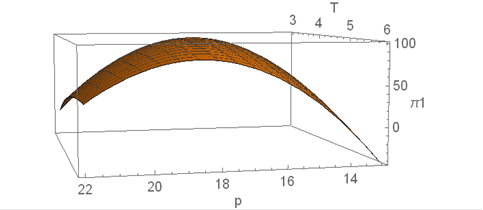
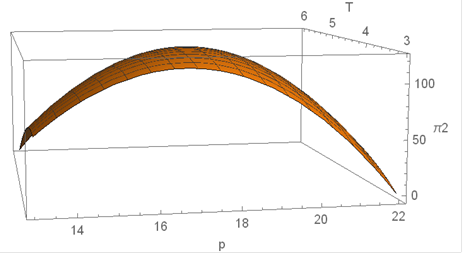
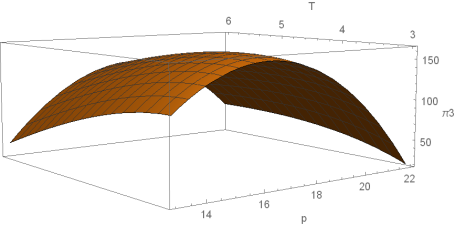
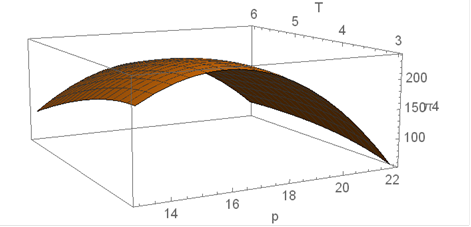
Now we show three-dimensional plotting of retailer’s average profit function with respect to two decision variables selling price and cycle length for Case1, Sub Case 2.1, Sub Case 2.2, Sub Case 2.3 respectively.

Figure 6 Profit function for Case 1 with respect to decision variables selling price (p) and cycle length (T)

Figure 7 Profit function for Sub Case 2.1 with respect to decision variables

Figure 8 Profit function for Sub Case 2.2 with respect to decision variables

Figure 9 Profit function for Sub Case 2.3 with respect to decision variables

 

All these diagrams ensure maximization of retailer’s profit function. This section has been performed with the help of MATHEMATICA SOFTWARE.

 

7.    CONCLUSION

In this work we have presented a mathematical model which maximizes retailer average profit depending on decision variables namely cycle time and selling price. Different situations associated with two stage trade credit have been considered. It has been observed from numerical results that retailer profit increases as length of the credit period offered by the bank increases. Here we take demand pattern based on selling price linearly.  This work may be extended by taking non-linear demand pattern. Also credit linked as well as selling price dependent demand pattern may be a possible extension of this modelling frame work.

 

REFERENCES

Abad, P.L. (1996), Optimal pricing and lot-sizing under conditions of perishability and partial backordering, Management Science, 42(8) :1093-1104. Retrieved from https://doi.org/10.1287/mnsc.42.8.1093

Abad, P.L. (2001), Optimal price and order size for a reseller under partial backordering, Computers and Operations Research, 28, 53-65. Retrieved from https://doi.org/10.1016/S0305-0548(99)00086-6

Chung, K-J, (2013), The EPQ model under conditions of two levels trade credit and limited storage capacity in supply chain management, International Journal of System Science,44(9),1675-1691. Retrieved from https://doi.org/10.1080/00207721.2012.669864

Chung, K-J, Cardenas-Barron, L.E., Ting, P-S., (2014), An inventory model withnon-instantaneous receipt and exponentially deteriorating item for an integrated three layer supply chain under two levels of trade credit, International Journal of Production Economics,155,310-317. Retrieved from https://doi.org/10.1016/j.ijpe.2013.12.033

Giri, B.C., Sharma, S., (2016), Optimal ordering policy for an inventory system with linearly increasing demand and allowable shortages under two levels of trade credit financing, Operational Research, 16(1),25-50. Retrieved from https://doi.org/10.1007/s12351-015-0184-y

Giri, B.C., Sharma, S., (2019), Optimising an integrated production-inventory system under cash discount and retailer partial trade credit policy. Journal of System Science : Operations and Logistics,6(2), 99-118. Retrieved from https://doi.org/10.1080/23302674.2017.1371358

Goyal, S.K. (1985), Economic order quantity under conditions of permissible delay in payments, Journal of Operational Research Society,36(4),335-338. Retrieved from  https://doi.org/10.1057/jors.1985.56

Harris, F.W. (1913), How many parts to make at once, Factory, The Magazine of Management,10(2) ,135-136.

Huang,Y-F.(2003),Optimal retailer's ordering policies in the EOQ model under trade credit financing, Journal of Operational Research Society,54,1011-1015. Retrieved from https://doi.org/10.1057/palgrave.jors.2601588

Jaggi,C.K., Goyal, S.K, Goel, S.K.,(2008), Retailer's optimal replenishment decisions with credit-linked demand under permissible delay in payments, European Journal of Operational Research, 190,130-135. Retrieved from https://doi.org/10.1016/j.ejor.2007.05.042

Mandal, A., Pal, B., Chaudhuri, K.S. (2020), Unrelaible EPQ model with variable demand under two-tier credit financing, Journal of Industrial and Production Engineering,37(7),370-386. Retrieved from https://doi.org/10.1080/21681015.2020.1815877

Pal, B. (2018), Optimal production model with quality sensitive market demand, partial backlogging and permissible delay in payment, RAIRO-Operations Research, 52, 499-512. Retrieved from https://doi.org/10.1051/ro/2017068

Pal, B., Mandal, A., Sana, S.S. (2021), Two-phase deteriorated supply chain model with variable demand and imperfect production process under two-stage credit financing. RAIRO-Operations Research, 55, 457-580. Retrieved from https://doi.org/10.1051/ro/2021008

Tiwary, S., Cardenas-Barron, L.E., Goh, M., Shaikh, A. A., (2018), Joint pricing and inventory model for deteriorating items with expiration dates and partial backlogging under two-level partial trade credits supply chain, International Journal of Production Economics,200,16-36. Retrieved from https://doi.org/10.1016/j.ijpe.2018.03.006