and Lenovo are famous for products that reach relatively low prices and features. Consumer’s preference for higher prices to quality will influence himself to buy Apple products which are regarded suitable for their requirements. By preferring features and prices, end-customers’ accommodate on product quality and buy Samsung or Lenovo products. The vendors need both advanced manufacturing processes and good quality raw materials if they want to produce high reliability products. To assemble laptops, Lenovo uses low cost raw-materials to reduce overall costs whereas Apple uses very high quality ingredients in MacBooks and hence overall costs increases. To optimize a firm’s profit, a balance needs to be struck between time, price and reliability of its product.

Integrated supply chain models have been developed in the literature based on some limited assumptions. One of these assumptions is that the vendor produces products of perfect quality. In fact, there can be a few imperfect items in any production lot due to poor control of processes, non-adherence to plans, inappropriate operating guidelines, and so on. If the vendor has to pay extra cost for each defective item produced then it is profitable to reduce the number of defective items in the production process. The rate of defective items produced by the vendor affects other critical decisions such as the vendor’s production lot size and reliability of the product. Further, a vendor has a reputation for making more reliable product which is preferable for a buyer to place an order. To improve the quality of a product, investment can be made to reduce errors in the vendor’s production process. In an integrated supply chain system, when non-conformable items are produced, it is most likely that some kind of supervision/inspection activity needs to be performed by the buyer before selling the goods to the end customers.

This article develops an integrated single-vendor single-buyer supply chain model with time, price and reliability dependent market demand. The vendor’s production process is imperfect and it rejects all the non-conformable items produced during a production run. The buyer screens all the items before selling to end-customers. The defective items are sold in the secondary market with a discount. The vendor plans for a lot-for-lot production policy to meet the buyer’s demand. The primary objectives of this article are to find the response of the following queries:

1)     How much time will be taken by the vendor and the buyer to produce a lot and sell to customers?

2)     How much time will be delayed by the vendor to produce items ordered by the buyer?

3)     What will be the selling price of each good item from the buyer’s side?

4)     What will be the reliability of a product produced by the vendor?

 

The rest of the paper is arranged as follows: In the next section, the related literatures are reviewed. Section 3 presents assumptions and notations for developing the proposed model. Section 4 discusses the mathematical model and solution procedure. A numerical example is provided in Section 5. The optimal results are analyzed in Section 6. Section 7 concludes the paper and indicates some future research directions. 

 

 

 

 

 

2.    LITERATURE REVIEW

In reality, the market demand of certain products may not remain constant always; it may change with the passage of time. Hariga and Benkherouf (1994) presented a heuristic inventory model in which the market demand changes exponentially in time over a finite planning horizon. Hariga (1996) developed an inventory lot-sizing model with time-varying demand for deteriorating items. An inventory model with Weibull deterioration, time proportional demand rate and effects of inflation was developed by Chen (1998). Khanra and Chaudhuri (2003) proposed an inventory model with quadratic time dependent demand where the on-hand inventory deteriorates with time.  Ghosh and Chaudhuri (2006) developed this model by considering shortages in inventory. Actually, a large volume of research papers on time dependent demand are available in the literature  Giri and Maiti (2012), Chowdhury et al. (2014), Samanta et al. (2018)

Now-a-days the customer’s demand depends not only on time but also on other factors such as product price, after sales service, advertisement, product quality, etc. Price of a product plays an important role in customer’s mind. So, it is more realistic to include price sensitive demand. Burwell  et al. (1991) determined the optimal lot size and selling price when a supplier offers all-unit quantity discounts by considering price-dependent demand and allowing for shortages. A finite period system was considered by Datta and Paul (2001) under multi-replenishment scenario, where the demand rate is influenced by both displayed stock level and selling price. An economic production quantity (EPQ) model for deteriorating items was developed by Teng and Chang (2005) where the demand rate depends on the selling price and display stock level with limited display space consideration. You (2005) investigated a supply chain model in which a leading member of the supply chain gets the scope to settle value of the product to impress demand and more revenues. Avinadav et al. (2013) formulated a model for finding the optimal pricing, order quantity and replenishment period for deteriorating items with price- and time-dependent demand. Yang et al. (2013) studied a piecewise production-inventory model for a deteriorating item with time-varying and price-sensitive demand to optimize the vendor’s total profit. Herbon and Khmelnitsky (2017) considered a dynamic pricing policy for perishable products, attracting customers to buy less-fresh products due to expiry, potentially increasing revenue and eliminating waste. Numerous works in this direction could be found in the literature  You and Hsieh (2007), Chen et al. (2010), Ghosh et al. (2011), Kim et al.  (2011),  Bhunia and Shaikh (2014), Maiti and Giri (2015), Giri and Roy (2015), Maiti and Giri (2017),  Chan (2019), Roy and Giri (2020).

When end-customers buy some goods from buyers, it is the outcome of the endeavors of several members of supply chains. But, the main credit goes to the vendor as the customer prefer that product for his reliability. So, the balance between price and reliability is an important factor in inventory/supply chain management. Therefore, the reliability of a product must be taken into consideration. An EPQ model with a flexible and imperfect production process was proposed by Cheng (1989) under reliability consideration. Sadjadi et al. (2009) considered a production-marketing problem where the reliability of the production process assumed to be imperfect and the inventory and the setup costs per production cycle are not known in advance. An inventory model with imperfect production process was developed by Shah and Shah (2014) for time-declining demand pattern where reliability of the production process was considered as a decision variable. Shah and Vaghela (2018) analysed EPQ model with time and advertisement sensitive demand with the effect of inflation and reliability.

The above works considered reliability of the product and its effect on the optimal results. However, none of these works would consider the market demand as a function of reliability of the product. Khara et al. (2017) considered a model that deals with an imperfect production process, where both perfect and imperfect quality items are produced and demand depends on selling price and reliability of the product. Later, Khara et al. (2019) developed that model by considering demand as a function of selling price, reliability of the product and advertisement cost. Shah and Naik (2020) investigated an inventory model with imperfect production process and reliability-dependent demand.

Chung and Wee (2008) developed an integrated production-inventory deteriorating model considering imperfect production, inspection planning and warranty-period-and stock-level-dependant demand. Jauhari (2016) proposed a vendor-buyer model where the lot transferred from the vendor to the buyer contains some defective items and the buyer conducts an imperfect inspection process to classify the quality of the items. Jauhari  et al. (2016) developed an imperfect production-inventory model where the buyer uses periodic review policy to manage his inventory. The demand on the buyer side was assumed to be normally distributed, and the shortage was assumed to be fully backordered and the defective rate of the items was assumed to be fixed.

In this article, we consider the market demand as a function of time, selling price and reliability of the product. The production rate is not constant but depends on the market demand, as considered by Giri and Maiti (2012). The variable production rate was also considered by Jauhari  et al. (2016). In the literature, unit production cost is considered as a fixed. But in reality, it should depends on order quantity to be produced by the vendor. More production implies less unit production cost and less production implies expensive production cost. On the other hand, if a vendor prefers to produce an item with more reliable to keep/increase his reputation in market, then (s)he has to use raw material which are also more reliable. Thus the material cost depends on reliability of the product. The demand may change at any time during production process. In that case, to maintain the on-time delivery to the buyer, the vendor’s production rate has to be changed. Therefore, we consider the unit production cost as a function of material cost and production rate. Variable unit production cost was also considered in different forms by Khara et al. (2017).

 

3.    MODEL ASSUMPTIONS AND NOTATIONS

The notations used throughout the paper are as follows:

	:	time interval between successive deliveries (decision variable)
	:	time delayed by the vendor to start production (decision variable)
	:	unit selling price for the buyer(decision variable)
	:	reliability of the product (decision variable)
	:	variable time
	:	number of cycles
	:	demand rate at the buyer
	:	production rate at the vendor
	:	scaling constant for production rate
	:	set up cost per production run for the vendor
	:	ordering cost per order for the buyer
	:	unit stock-holding cost per unit per unit time for the vendor
	:	unit stock-holding cost per unit per unit time for the buyer
	:	quantity produced by the vendor during the period
	:	market demand during the period
	:	material cost
	:	price elasticity to demand
	:	reliability elasticity to demand
	:	reliability elasticity to material cost
	:	fixed material cost
	:	material cost increases the reliability of the produced item
	:	variation constant of tool/die costs
	:	transportation cost per shipment
	:	unit production cost
	:	screening rate
	:	unit screening cost
	:	unit wholesale price for the vendor
	:	discount price per defective item for the vendor
	:	buyer’s inventory level
	:	vendor’s inventory level
	:	buyer’s profit function
	:	vendor’s profit function
	:	average total profit to the whole supply chain

 

The following assumptions are made to develop the proposed integrated vendor-buyer inventory model:

·        The supply chain consists of a single-vendor and a single-buyer who stocks and sells a single product.

·        The demand for a product depends on time  selling price  as well as the reliability of the product . We assume that the demand rate  and  are real constants. This type of demand was considered by Khara et al. (2017).

·        The vendor follows the lot-for-lot policy for replenishment made to the buyer.

·        The buyer receives the first order from the vendor at time  and (s)he receives order from the vendor in every  time interval.

·        Shortages are not allowed in the buyer’s inventory.

·        As the reliability of the product depends not only on the manufacturing system but also on the quality of the raw material of the product, we assume that the material cost  is an increasing function of the reliability () of the product such that   where  and .

·        The production rate of the vendor varies with the demand rate. Also, the production rate is greater than the demand rate. We take the production rate  as   where .

·        As the vendor’s production rate is greater than the buyer’s demand rate, the vendor may start production with a time delay  in the n-th production cycle.

·        The production cost not only depends on the material cost  but also on tool or die cost, which is proportional to the vendor’s production rate. Therefore, the unit production cost  is assumed as  where .

·        The vendor’s production process is not perfectly reliable. During a production run, it may produce some defective (non-conforming) items.

·        The buyer starts error-free screening after received products from vendor. We assume that the number of perfect units is at least equal to the demand during the screening time.

·        Product quality may be imperfect. In other words, only  of all produced items meet the demand while  of items are defective. It is apparent that the maximum reliability of the production process cannot exceed . This type of assumption was also considered by Sadjadi  et al. (2009).

·        The vendor produced  quantity in total during n-th production cycle and delivered to the buyer to meet the customer / market demand  in the next cycle.

 

4.    MODEL FORMULATION

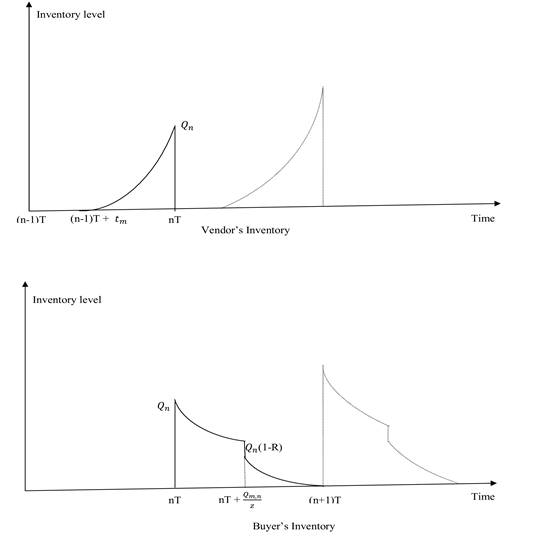
The graphical presentation of the vendor-buyer model is shown in Figure 1. We suppose that  is the length of each cycle. For the -th cycle, the vendor starts his/her production at time  and the buyer receives his/her order of quantity  from the vendor at time ,  and meets the market demand  for period . The buyer starts screening at a rate of  units per unit time immediately after receiving the products from the buyer. The buyer’s screening is completed at time . We assume that only  of received products are acceptable as good products to meet the customer demand. The customer’s demand rate at time  is  where  and  are real constants. 

Therefore, the total demand during the period  is given by

 

  (1)

 

Figure 1 A schematic diagram to represent the vendor’s and the buyer’s inventory.

 

The quantity  produced by the vendor in the time interval  is given by

         

          (2)

 

4.1. DECENTRALISED MODEL

4.1.1.  VENDOR’S PERSPECTIVE

Let  be the vendor’s inventory level at any time . Then the instantaneous states of the vendor’s inventory level can be described by the differential equation:

 

  (3)

 

 Solving (3), we get

 

 

(4)

 

 At time , we have

         

                 

 

 The vendor’s holding cost per unit time for the period

 

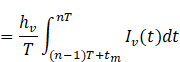
 The vendor’s production cost per unit time in that period

 

 

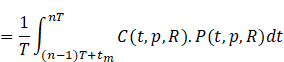
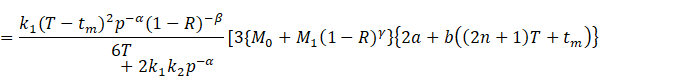
 As the vendor’s sales revenue =  set-up cost , discount cost for defective items per unit time = , therefore, the vendor’s total profit per unit time is given by

        

                 

 

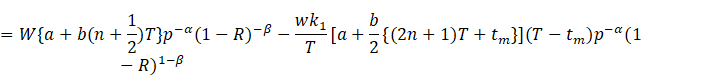
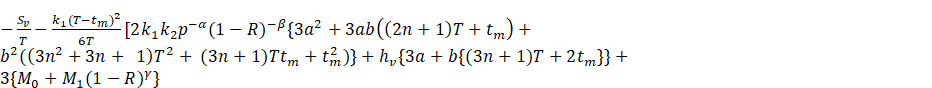
                                                                 (5)

 

 

 

 

4.1.2.  BUYER’S PERSPECTIVE

 

The differential equation governing the buyer’s inventory level at any time is given by

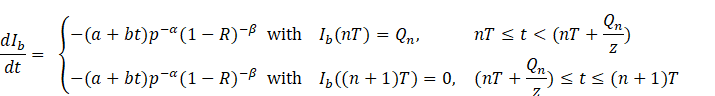
Solving, we get

 

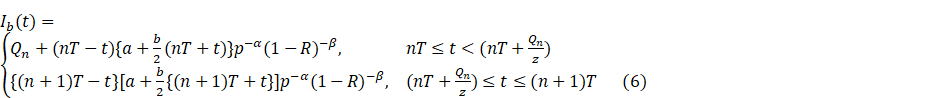
From (6), the buyer’s inventory level at the time pointis given by

 

                                                     (7)

 

Also, we have

 

                            (8)

 

From (7) and (8), we have

 

                                           (9)

 

Which is a quadratic equation in  with discriminant

 

.

 

Hence there always exists a positive (real) production lot size  of the vendor in any time interval , for all .

 

Now, the buyer’s holding cost per unit time

 

Also, sales revenue per unit time = , purchase cost per unit time =, transportation cost per unit time = , screening cost per unit time =  and ordering cost per unit time = . Therefore, the buyer’s total profit per unit time is given by

    

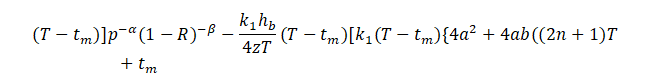
                                                                                    (10)

 

Proposition 1  When the buyer’s selling price  is known, the profit function  is concave with respect to  for all   where

         

         

         

 provided that

Proof. Differentiating (10) twice with respect to , we get

              

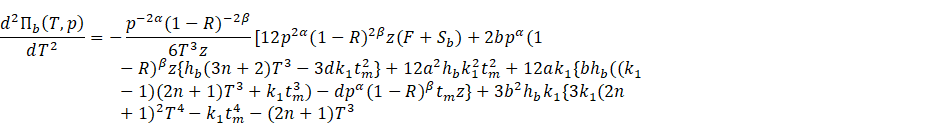
It is clear from the above that  provided that

 which gives  (say)

 which gives

             or,  (say)

or,

or, [since ]

or,

or, (say)

Hence the proposition is proved.

 

Proposition 2  For  where  and

, the profit function  is concave with respect to  for all  satisfying the condition

Proof. Differentiating (10) twice with respect to , we get

         

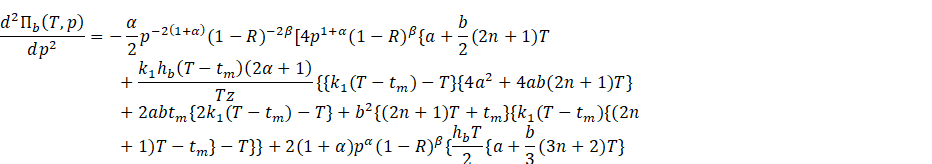
From above,  provided that the following conditions hold:

 which implies .

Considering the above inequation as equation, we see that the two roots of the equation are

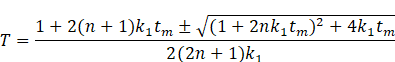
We take  such that.

As the buyer’s selling price  is always greater than the vendor’s wholesale price , we have . Hence, the proposition is proved.

 

Proposition 3  For known ,  and , the vendor’s profit function  is concave with respect to  if  provided that .

Proof. Differentiating (5) twice with respect to , we get

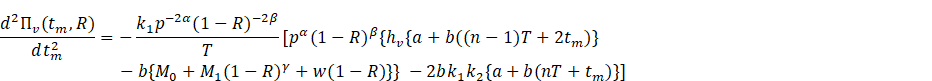
Clearly, if

If , then from above we have,

Again, if , then from above we have,

This proves the proposition.

 

Proposition 4   For known , the profit function  is concave with respect to  for all  where,  and .

 

Proof. Differentiating (5) twice with respect to , we get

       

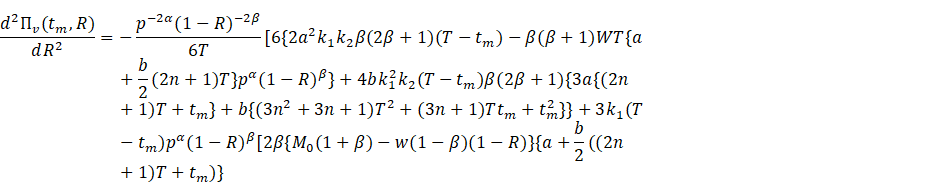
Clearly, the profit function  will be concave with respect to  if the following two conditions are satisfied:

     

From  we have

From  we have

Hence, the proposition is proved.

 

4.2. CENTRALISED MODEL

The average total profit of the integrated supply chain is given by

         

         

     

      

       

             (11)

 

Proposition 5  In case of the centralized supply chain system, the product reliability  depends on the decision variables  and  given by the relation

 

                                                                          (12)

 

Proof. The vendor delivers  quantity of items to the buyer, of which  is found to be defective after completion of the buyer’s screening process. Hence, only  quantity is considered as good items and sold by the buyer to meet the market demand . Since, there is no shortage and no excess items, we can claim that  Using (1) and (2), we have

 

 

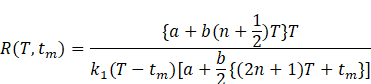
Proposition 6  The buyer’s selling price  depends on the decision variables  and  given by the relation                  (13)

where  is given by (12).

 

Proof. Substituting the value of  from (2) into the relation (9), we get

                         

                   

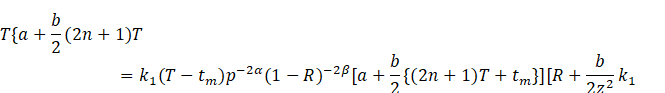
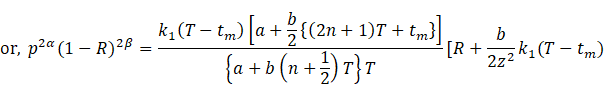
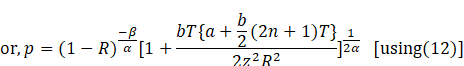
Hence, the proposition is proved.

 

Proposition 7 To meet the customer demand , the vendor produces  quantity of items with delay in time  satisfying the relation

 

 

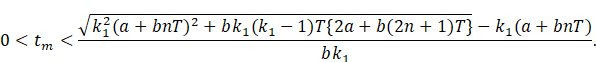
Proof.  Since , therefore, from (12) it is obvious that .

Again,  gives

or,

Considering the above inequation as equation, we see that the two roots of the equation are

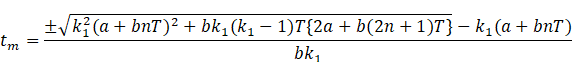
The smaller root is negative and hence the proposition is proved.

 

Using (12) and (13), the profit function  can be reduced to the function  of two independent variables  and . It is not possible to prove analytically that  is jointly concave. However, we can prove the following proposition:

 

 

 

Proposition 8  For known values of  and , the profit function  is concave with respect to  for all  according as and  satisfies the relation  where,

 

Proof. Differentiating (11) twice with respect to , we get

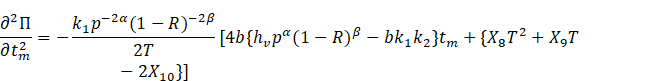
The profit function  will be concave with respect to  if

For , we have.

Since the vendor’s production delay time  is always positive, the numerator of the right hand expression must be positive and hence . This proves the proposition.

 

Proposition 9  For pre-defined values of  and , the profit function  is concave with respect to  if

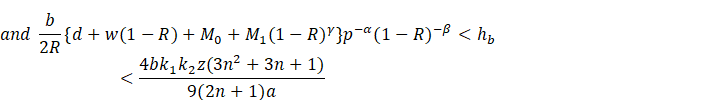
Proof. Differentiating (11) twice with respect to , we have

 

         

         

         

         

 

In the right-hand side of the above equation, the expression within the third bracket will be positive if the following three conditions are satisfied:

From  we have, .

From  we have,  provided that

From  we have .

Hence, the proposition is proved.

 

5.    NUMERICAL EXAMPLE

To illustrate the developed models numerically, we consider the following data-set (Giri and Maiti (2012)):

 and . Also, we consider  in appropriate units.

 

To check the concavity of the profit function , we observe that  and  have to satisfy the conditionsand the variable  has no restriction. So, we consider and  The decision variables and are found from the propositions 6 and 7, respectively as  and . Then we have,  and the determinant of Hessian matrix associate with  is given by

 

         

 

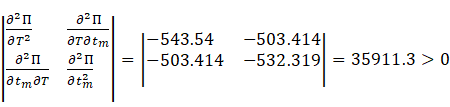
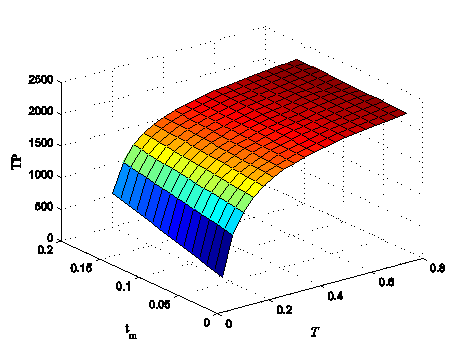
This proves that, for the above data set, the profit function  is concave in  and . One evidence is shown in Figure 2 for . We observe that, if we move from one cycle to the next cycle, the buyer’s ordering time period  and the vendor’s delay time  to start production change very slowly whereas the average total profit of the supply chain increases considerably. Without any loss of generality, we consider the sixth cycle  and we obtain  and . In this sixth cycle, the vendor produces  quantity of items. After receiving these items, the buyer performs screening and  of  quantity of items is considered as good quality and perfect items to meet the demand  given by (1). 

Figure 2 Graphical representation of the profit function  for

 

The buyer’s selling price , the product reliability  and the average total profit of the supply chain increase as we move from one cycle to the next cycle. Since the changes inand are insensitive, we present in Table 1 the values of  and  for successive ten cycles.

Table 1 Optimal results of the proposed model for successive ten cycles
-th cycle
1	12.9386	0.874390	2035.33
2	12.9523	0.837046	2053.32
3	12.9660	0.837050	2071.32
4	12.9798	0.837055	2089.34
5	12.9935	0.837059	2107.37
6	13.0073	0.837063	2125.42
7	13.0210	0.837068	2143.48
8	13.0348	0.837072	2161.56
9	13.0485	0.837076	2179.66
10	13.0623	0.837080	2197.77

 

5.1. THE CASE OF

In this scenario, we assume that the demand rate depends on time only and hence we put  and  in our proposed model. The demand rate becomes  and the vendor’s production rate is  with  Also, we assume that unit production cost does not depend on reliability and it is fixed and denoted by . To compare the results with the optimal results of our proposed model, we take ,  and . This

 

 

Table 2 Comparison of the results of our model and the model with
	Model with			Our model	Difference of profits
-th cycle
1	3.19089	1.06363	1016.77	2035.33	1018.56
2	4.10970	1.36990	1052.09	2053.32	1001.23
3	4.91770	1.63923	1092.64	2071.32	978.68
4	5.32066	1.77355	1134.25	2089.34	955.09
5	5.44683	1.81561	1174.16	2107.37	933.21
6	5.43545	1.81182	1211.56	2125.42	913.86
7	5.35954	1.78651	1246.45	2143.48	897.03
8	5.25452	1.75151	1279.06	2161.56	882.50
9	5.13785	1.71262	1309.67	2179.60	869.93
10	5.01832	1.67277	1338.52	2197.77	859.25

 

implies that  of received items from the vendor is sold by the buyer at the retail price  to meet the market demand. All the remaining assumptions are kept unchanged. Thus, we take ,  and  and all other parameter-values are same as assumed before. With this data-set, we find that for ,  and the average total profit of the supply chain as  which is $2125.42 less than that of our proposed model. In Table 2, we compare the optimal results of ten successive cycles with those of the proposed model.

 

5.2. THE CASE OF

Here we assume that the vendor’s produced items are all perfect, although in reality it may not always happen. To compare the results with those of the proposed model, we assume the market

Table 3 Comparison of profits of the proposed model and our model with
Model with				Our model	Difference of profits
-th cycle
1	4.10977	1.36992	729.98	2035.33	1305.35
2	5.99780	1.99927	765.33	2053.32	1287.99
3	8.86478	2.95493	815.01	2071.32	1256.31
4	11.4611	3.82038	878.73	2089.34	1210.61
5	13.3829	4.46097	951.72	2107.37	1155.65
6	14.7948	4.93159	1030.37	2125.42	1095.05
7	15.8619	5.28731	1112.63	2143.48	1030.85
8	16.6930	5.56433	1197.30	2161.56	964.26
9	17.3571	5.78570	1283.65	2179.60	895.95
10	17.8994	5.96648	1371.22	2197.77	826.55

demand as , where  and . The production rate is  with  In this case, the buyer’s holding cost changes to . As before, we assume that unit production cost . Since, all products are perfect, there is no need to screen and hence we take  and . All the remaining assumptions are kept unchanged. Thus, in numerical data, we take ,  and , keeping all other parameter-values unchanged. From the numerical experiment, we find that ,  and the average total profit of the supply chain model is , which is  less than that of our proposed model. In Table 3, we compare the optimal results of ten successive cycles with those of our proposed model. 

 

6.    SENSITIVITY ANALYSIS

In this section, we investigate the effect of change of one parameter-value at a time keeping the remaining parameter-values unchanged. The sensitivity of the parameters  and  are shown in the Figure 3, Figure 4, Figure 5, Figure 6, Figure 7. Some insights from our investigation are given below.

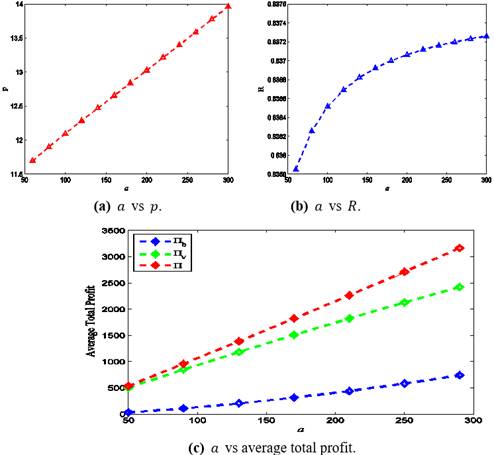
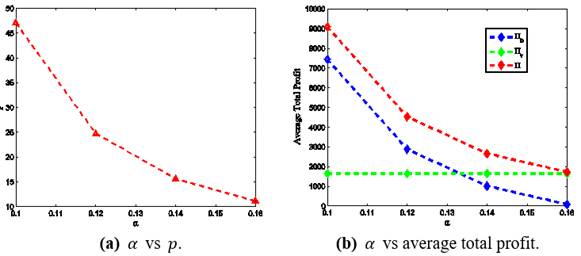
1)    Both the buyer’s selling price  and the product reliability  increase rapidly as  increases (Figure 3). The vendor has to produce more reliable product as  increases. As a result, the vendor’s unit production cost increases and at the same time, the market

Figure 3 Change (%) in optimal results w.r.t. .

demand also increases. Therefore, the buyer’s average total profit as well as the vendor’s average total profit increase as  increases. Consequently the average total profit of the integrated supply chain increases as  increases (Figure 3 ).

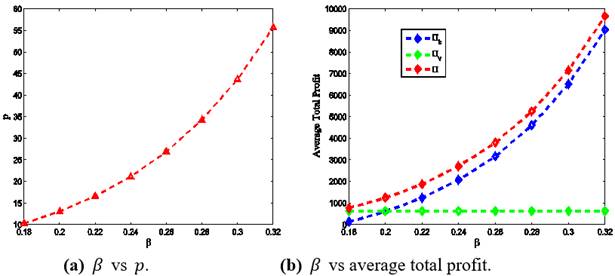
2)    As  increases, the selling price  increases but the rate of increase in  is not so high. The buyer’s average total profit increases significantly but the vendor’s average total profit increase is very low. As a result, the average total profit of the integrated supply chain model increases moderately as the value of  increases (Figure 4 ).

Figure 4 Change (%) in optimal results w.r.t. .

 

3)    The product reliability  is not affected by the price elasticity to demand  but the buyer’s selling price is highly sensitive with respect to  as shown in Figure 5. A  increase in the value of  results  decrease in the value of the selling price . But it does not have any impact on the vendor’s average total profit. A lower selling price results in lower profit from the buyer’s perspective as well as from the integrated supply chain’s perspective (Figure 5 ).

Figure 5 Change (%) in optimal results w.r.t. .

 

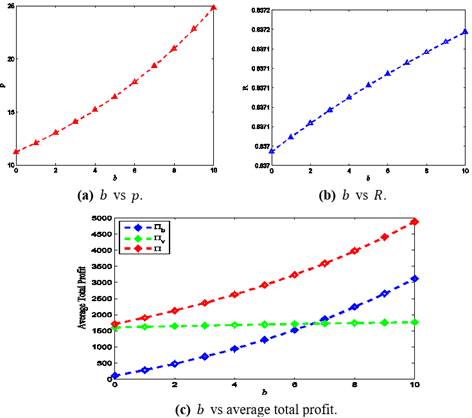
4)    As  increases, the selling price  and the average total profits of the buyer and the entire supply chain increase (Figure 6).

Figure 6 Change (%) in optimal results w.r.t. .

 

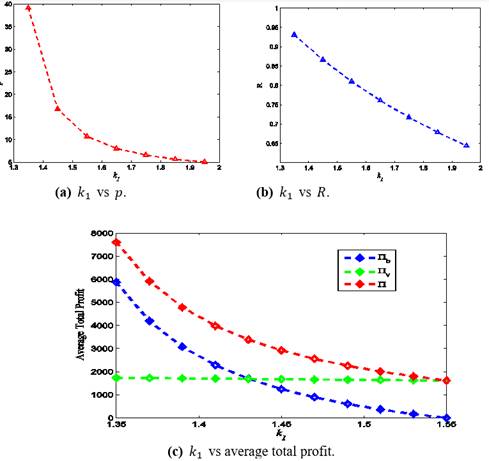
5)    Figure 7 shows that, as  increases, the buyer’s selling price and reliability of the product decrease (Figure 7). Due to increase in production rate, the vendor’s production time decreases but there is at most no change in the average total profit of the vendor. However, the average total profit of integrated supply chain decreases as  increases (Figure 7).

Figure 7 Change (%) in optimal results w.r.t. .

 

 

 

7.    CONCLUSION

The paper considers a single vendor single buyer integrated supply chain model in which the market demand is assumed to be dependent on time, price and reliability of the product. The vendor follows a lot-for-lot policy. The items are delivered to the buyer with an agreement that the buyer himself screens all those products and, if any item is found defective, it should be sold with price discount and the cost must be borne by the vendor. The reputation of the vendor and the buyer increase as the product bears good and perfect quality to the best of their knowledge. On the other hand, the end customer’s satisfaction increases as the product is more reliable. In this paper, some propositions are derived which help to choose the data-set in the numerical example as well as to find the optimal values of the decision variables. From the numerical analysis, we have found that the vendor has to maintain the reliability of the product and produce items not more  defective. It is also observed that the scaling constant  for the demand act important roles to increase the profits of the buyer, vendor and the integrated supply chain.

In this article, we have assumed a deterministic market demand, which has limited applications in the business world. So, this model can be extended by considering stochastic demand. Shortages are not allowed in our model. So, one can extend the present model with inclusion of shortage in the buyer’s inventory. One can also consider multi-vendor and/or multi-buyer supply chain for further study. Terms and conditions may be imposed by the vendor to sell the defective items (from buyer’s screening) with price discount.

 

REFERENCES

A Bhunia and A Shaikh (2014). A deterministic inventory model for deteriorating items with selling price dependent demand and three-parameter Weibull distributed deterioration. International Journal of Industrial Engineering Computations, 5(3):497-510. Retrieved from https://doi.org/10.5267/j.ijiec.2014.2.002

Avi Herbon and Eugene Khmelnitsky (2017). Optimal dynamic pricing and ordering of a perishable product under additive effects of price and time on demand. European Journal of Operational Research, 260(2): 546-556. Retrieved from https://doi.org/10.1016/j.ejor.2016.12.033

B Samanta, Bibhas C Giri, and K S Chaudhuri (2018). A Vendor-Buyer Supply Chain Model for Deteriorating Item with Quadratic Time-Varying Demand and Pro-rata Warranty Policy. In International workshop of Mathematical Analysis and Applications in Modeling, pages 371-383. Springer. Retrieved from https://doi.org/10.1007/978-981-15-0422-8_31

Balaji Roy and Bibhas C Giri (2020). A three-echelon supply chain model with price and two-level quality dependent demand. RAIRO-Operations Research, 54(1):37-52. Retrieved from https://doi.org/10.1051/ro/2018066

Barun Khara, Jayanta Kumar Dey, and Shyamal Kumar Mondal (2017). An inventory model under development cost-dependent imperfect production and reliability-dependent demand. Journal of Management Analytics, 4(3):258-275. Retrieved from https://doi.org/10.1080/23270012.2017.1344939

Barun Khara, Jayanta Kumar Dey, and Shyamal Kumar Mondal (2019). Effects of product reliability dependent demand in an EPQ model considering partially imperfect production. International Journal of Mathematics in Operational Research, 15(2):242-264. Retrieved from https://doi.org/10.1504/IJMOR.2019.10022969

Bibhas C Giri and B Roy (2015). A single-manufacturer multi-buyer supply chain inventory model with controllable lead time and price-sensitive demand. Journal of Industrial and Production Engineering, 32(8):516-527. Retrieved from https://doi.org/10.1080/21681015.2015.1086442

Bibhas C Giri and T Maiti (2012). Supply chain model for a deteriorating product with time-varying demand and production rate. Journal of the Operational Research Society, 63(5): 665-673. Retrieved from https://doi.org/10.1057/jors.2011.54

C J Chung and H-M Wee (2008). An integrated production-inventory deteriorating model for pricing policy considering imperfect production, inspection planning and warranty-period-and stock-level-dependant demand. International Journal of Systems Science, 39(8):823-837. Retrieved from https://doi.org/10.1080/00207720801902598

Haoya Chen, Youhua Frank Chen, Chun-Hung Chiu, Tsan-Ming Choi, and Suresh Sethi (2010). Coordination mechanism for the supply chain with leadtime consideration and price-dependent demand. European Journal of Operational Research, 203(1):70-80. Retrieved from https://doi.org/10.1016/j.ejor.2009.07.002

Hau-Ling Chan (2019). Supply chain coordination with inventory and pricing decisions. International Journal of Inventory Research, 5(3):234-250. Retrieved from https://doi.org/10.1504/IJIR.2019.10020307

Jen-Ming Chen (1998). An inventory model for deteriorating items with time-proportional demand and shortages under inflation and time discounting. International Journal of Production Economics, 55(1):21-30. Retrieved from https://doi.org/10.1016/S0925-5273(98)00011-5

Jinn-Tsair Teng and Chun-Tao Chang (2005). Economic production quantity models for deteriorating items with price-and stock-dependent demand. Computers & Operations Research, 32(2):297-308. Retrieved from https://doi.org/10.1016/S0305-0548(03)00237-5

Jungkyu Kim, Yushin Hong, and Taebok Kim (2011). Pricing and ordering policies for price-dependent demand in a supply chain of a single retailer and a single manufacturer. International Journal of Systems Science, 42(1):81-89. Retrieved from https://doi.org/10.1080/00207720903470122

Moncer A Hariga and Lakdere Benkherouf (1994). Optimal and heuristic inventory replenishment models for deteriorating items with exponential time-varying demand. European Journal of Operational Research, 79(1):123-137. Retrieved from https://doi.org/10.1016/0377-2217(94)90400-6

Moncer Hariga (1996). Optimal EOQ models for deteriorating items with time-varying demand. Journal of the Operational Research Society, 47(10):1228-1246. Retrieved from https://doi.org/10.1057/jors.1996.151

Nita H Shah and Bhavin J Shah (2014). EPQ model for time-declining demand with imperfect production process under inflationary conditions and reliability. International Journal of Operations Research, 11(3):91-99.

Nita H Shah and Chetansinh R Vaghela (2018). Imperfect production inventory model for time and effort dependent demand under inflation and maximum reliability. International Journal of Systems Science: Operations & Logistics, 5(1):60-68. Retrieved from https://doi.org/10.1080/23302674.2016.1229076

Nita H Shah and Monika K Naik (2020). Inventory Policies with Development Cost for Imperfect Production and Price-Stock Reliability-Dependent Demand. In Optimization and Inventory Management, pages 119-136. Springer. Retrieved from https://doi.org/10.1007/978-981-13-9698-4_7

P S You (2005). Inventory policy for products with price and time-dependent demands. Journal of the Operational Research Society, 56(7):870-873, Retrieved from https://doi.org/10.1057/palgrave.jors.2601905

Peng-Sheng You and Yi-Chih Hsieh (2007). An EOQ model with stock and price sensitive demand. Mathematical and Computer Modelling, 45(7-8):933-942. Retrieved from https://doi.org/10.1016/j.mcm.2006.09.003

Po-Chung Yang, Hui-Ming Wee, Shen-Lian Chung, and Yong-Yan Huang (2013). Pricing and replenishment strategy for a multi-market deteriorating product with time-varying and price-sensitive demand. Journal of Industrial & Management Optimization, 9(4):769. Retrieved from https://doi.org/10.3934/jimo.2013.9.769

R Roy Chowdhury, S K Ghosh, and K S Chaudhuri (2014). An order-level inventory model for a deteriorating item with time-quadratic demand and time-dependent partial backlogging with shortages in all cycles. American Journal of Mathematical and Management Sciences, 33(2):75-97. Retrieved from https://doi.org/10.1080/01966324.2014.881173

S K Ghosh and K S Chaudhuri (2006). An EOQ model with a quadratic demand, time-proportional deterioration and shortages in all cycles.International Journal of Systems Science, 37(10):663-672. Retrieved from https://doi.org/10.1080/00207720600568145

S K Ghosh, Sudhansu Khanra, and K S Chaudhuri (2011). Optimal price and lot size determination for a perishable product under conditions of finite production, partial backordering and lost sale. Applied Mathematics and Computation, 217(13):6047-6053. Retrieved from https://doi.org/10.1016/j.amc.2010.12.050

Seyed J Sadjadi, Mir-Bahador Aryanezhad, and Armin Jabbarzadeh (2009). An integrated pricing and lot sizing model with reliability consideration. In 2009 International Conference on Computers & Industrial Engineering, pages 808-813. IEEE. Retrieved from https://doi.org/10.1109/ICCIE.2009.5223880

Sudhansu Khanra and K S Chaudhuri (2003). A note on an order-level inventory model for a deteriorating item with time-dependent quadratic demand. Computers & Operations Research, 30(12):1901-1916. Retrieved from https://doi.org/10.1016/S0305-0548(02)00113-2

TCE Cheng (1989). An economic production quantity model with flexibility and reliability considerations. European Journal of Operational Research, 39(2):174-179. Retrieved from https://doi.org/10.1016/0377-2217(89)90190-2

Tal Avinadav, Avi Herbon, and Uriel Spiegel (2013). Optimal inventory policy for a perishable item with demand function sensitive to price and time. International Journal of Production Economics, 144(2):497-506. Retrieved from https://doi.org/10.1016/j.ijpe.2013.03.022

Tapan Kumar Datta and Karabi Paul (2001). An inventory system with stock-dependent, price-sensitive demand rate. Production planning \& control, 12(1):13-20. Retrieved from https://doi.org/10.1080/09537280150203933

Tarun Maiti and Bibhas C Giri (2015). A closed loop supply chain under retail price and product quality dependent demand. Journal of Manufacturing Systems, 37:624-637. Retrieved from https://doi.org/10.1016/j.jmsy.2014.09.009

Tarun Maiti and Bibhas C Giri (2017). Two-period pricing and decision strategies in a two-echelon supply chain under price-dependent demand. Applied Mathematical Modelling, 42:655-674. Retrieved from https://doi.org/10.1016/j.apm.2016.10.051

Timothy H Burwell, Dinesh S Dave, Kathy E Fitzpatrick, and Melvin R Roy (1991). An inventory model with planned shortages and price dependent demand.Decision Sciences, 22(5):1187-1191. Retrieved from https://doi.org/10.1111/j.1540-5915.1991.tb01916.x

Wakhid Ahmad Jauhari, Nelita Putri Sejati, and Cucuk Nur Rosyidi (2016). A collaborative supply chain inventory model with defective items, adjusted production rate and variable lead time. International Journal of Procurement Management, 9(6):733-750. Retrieved from https://doi.org/10.1504/IJPM.2016.10000438

Wakhid Ahmad Jauhari (2016). Integrated vendor-buyer model with defective items, inspection error and stochastic demand. International Journal of Mathematics in Operational Research, 8(3):342-359. Retrieved from https://doi.org/10.1504/IJMOR.2016.075520