Currently, there are many dimensional-reduction methods for hyperspectral image classification.  For example, the fuzzy C-means and gray scale optimization method was proposed in literature Jiang X. Linear (2011).  The subsection principal component analysis method was proposed in literature Kefeng Li, Quanzhen Huang (2019).  The salient feature extraction method was proposed in literature Md Rashedul Islam, Boshir Ahmed, Md Ali Hossain (2019).  A spectral spatial hyperspectral image classification method based on multi-scale conservative smoothing and adaptive sparse representation was proposed in literature Ren R, Bao W. (2019).  Literature Venkatesan R, Prabu S. (2019) proposed to use deep learning recursive neural network to classify features of hyperspectral images.  The spectral spatial feature extraction method for hyperspectral image classification was proposed in literature Wang A, Wang Y, Chen Y (2019).  

The above method of band selection is carried out in its original space.  In fact, high-dimensional data is usually not evenly distributed in its original space, but in its embedded low-dimensional subspace Wei Li, Yan Huang, C.-C (2017), Xiangpo Wei, Xuchu Yu, Bing Liu (2019).  For example, face image data under different illumination Zhang J, Li C G, You C (2019), moving tracks of objects in videos Zhao W, Du S. (2016) etc.  Therefore, this paper proposes a hyperspectral image classification method based on subspace clustering.  Based on the self-expression property of the data, the sparse representation of each band image is obtained through a global sparse optimization process.  Based on the sparse representation, the similarity matrix between the band images is established, and the spectral clustering algorithm is used to cluster the band images.  Then, a band is selected from each category to form a subset of bands, and the dimension reduction of hyperspectral data is completed. SVM classifier is used to classify and identify ground objects on the dimensionless sample points.  The experimental data show that the new method can effectively improve the accuracy of ground object recognition compared with other band selection methods.

 

2.    Hyperspectral image classification process

The space-borne hyperspectral imager is able to capture spectral signals from the earth's surface in different bands as it travels along the geostationary satellite orbit.  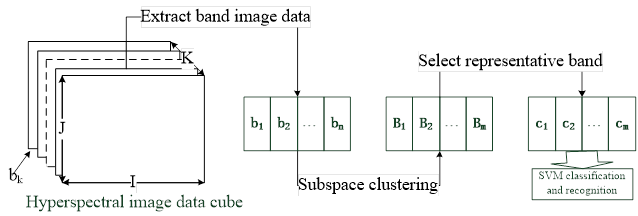Because the absorptance and reflectance of signals in the same band are different for different substances on the surface, the spaceborne hyperspectral imager obtains two-dimensional images of different bands, and two-dimensional images of all bands constitute a data cube, as shown in Figure 1.  

The left side of Figure 1 represents a hyperspectral image data cube, and each layer in the figure corresponds to a two-dimensional image of a band.  The cube has three dimensions, I, J and K. I and J represent the length and width of the two-dimensional image of the band.  K stands for spectral dimension.  Each pixel in the 3D data can be regarded as the reflection intensity of a surface substance (such as soil, desert, city, etc.) to different bands of spectral signals.  Because different substances have different reflectance to spectral signals of different bands, the relationship curve between spectral bands and spectral values of pixels can be drawn, which is called spectral curve.  According to different spectral curves, different surface materials in hyperspectral images can be classified.  A waveband image signal is represented as b_k.  The spectral curve of a pixel is represented as a vector p of K dimensions.  

 

Figure 1 Hyperspectral image classification process

Given a hyperspectral image data set B=[b₁,b₂,...,b_n], where each column represents the image data of a band, the subspace clustering method is used to cluster the image data of all bands to obtain the clusters {B₁,B₂,...B_m}. And then the cluster center is selected as the representative band c_i in each clusters to form the band subset {c₁,c₂,...c_m}, from which the hyperspectral pixel features p are constructed.  Thus, the dimension reduction of hyperspectral image pixel features is completed, and the hyperspectral pixels are classified and recognized by SVM classification method on the dimensional-reduction data.

 

3.    Band image clustering

In machine learning, signal and image processing, computer vision, pattern recognition and other applications, high-dimensional data is everywhere.  Images have millions of pixels, video data has millions of data frames, and text data has thousands of features.  High-dimensional data not only increases the spatial and temporal complexity of the algorithm, but also reduces the accuracy of classification and recognition, which is commonly called the "dimensional disaster" problem.  However, high-dimensional data are usually not evenly distributed in the feature space, but in the embedded low-dimensional subspace. Finding the low-dimensional subspace is not only beneficial to reduce the space-time complexity of the algorithm, but also can improve the accuracy of classification and recognition.  In this paper, each band image is regarded as a data point and subspace clustering method is used to cluster the band image data.  Then, a representative band is selected from each class to form a subset of the band to realize dimension reduction of hyperspectral image data.

Assume that U={u₁,u₂,…,u_m} represents linear subspace, where u_i represents the ith subspace.  The dimensions of the subspace are represented as D={d₁,d₂,…,d_m}, where, the dimensions of the ith subspace are represented as d_i.  The image data of all bands are represented as B=[b₁,b₂,...,b_n], where b_i represents the image data of the ith band.  

Subspace clustering algorithm can calculate the number and dimension of subspace, and can cluster the original band image data.  The clustering process is divided into two steps.  Firstly, for each band image, a global sparse optimization method is used to find the information encoding in the subspace.  Then, the similarity matrix is constructed with the information, and the original data is clustered by spectral clustering method.  

 

 

3.1.        GLOBAL SPARSE OPTIMIZATION

According to the self-expression attribute of data, the image of each band can be represented as a linear combination of the images of other bands: .  Among them, .  When the number of band images in subspace is larger than the subspace dimension  , the solution of this problem is not unique.  Among all the solutions, there is a sparse solution whose non-zero elements correspond to data points from the same subspace, and whose number of non-zero elements corresponds to the dimensions of the subspace .  That is, a band image data point from the  dimension subspace can be represented as a linear combination of  other band images from the subspace .  In order to obtain this sparse solution, the design optimization problem is as follows:  

 

        Equation 1

   

Therein,represents norm. For all band images, the global sparse optimization problem is designed as follows:

 

    Equation 2

 

Therein, is the coefficient matrix, each column of which corresponds to a sparse representation of a band image.   is the diagonal element of the matrix .  

 

3.2.        Spectral clustering

The sparse representation  of each band image data  is obtained by optimizing the problem (2). Non-zero elements of  correspond to data points from the same subspace, and the number of non-zero elements corresponds to the dimensions of the subspace.  With these sparse expression vectors, the spectral clustering method can be used to cluster the band image.  The undirected weighted graph is first established , wherein,  is the set of vertices, each vertex corresponds to a band image data point.  is the set of edges, each edge  has a weight  that represents the similarity of the vertices  and.  All the similarities form the similarity matrix , which is a non-negative symmetric matrix. Let , The similarity of the vertices  and is defined as. On the basis of weighted graph and similarity matrix, spectral clustering method is used to cluster the band image data. The pseudo-code of subspace clustering based band Selection algorithm (SCBS) is as follows:  

 

Algorithm 1：SCBS

Input: Collection of images in hyperspectral image data ;

Step 1: Solve the global sparse optimization problem (2) and obtain the sparse representation  of the band image;

Step 2: Construct undirected weighted graph ,Calculate its similarity matrix ;

Step 3: On the basis of similarity matrix, spectral clustering algorithm is applied to obtain band image clustering ;

Step 4: The cluster center of each cluster is selected to form the band feature subset  ;

Output: Feature set of selected bands .

 

4.    RESULTS AND DISCUSSIONS

In order to verify the effectiveness of the hyperspectral image classification method (SCBS) based on subspace clustering, experiments were carried out on real hyperspectral data sets.  The hyperspectral data set Pavia University was selected.  Pavia University data is hyperspectral data taken by the German Reflective Optics Spectrographic Imaging System (ROSIS-03) on the University of Pavia, Italy.  The spectral imager can continuously image 115 bands in the wavelength range of 0.43 to 0.86μm, and the spatial resolution of the image is 1.3m.  Among them, 12 bands are eliminated due to the influence of noise, so generally the image formed by the remaining 103 spectral bands is used.  The size of this data is 610×340, so it contains a total of 207,400 pixels. However, it contains a large number of background pixels and only 42,776 pixels containing ground objects. These pixels contain a total of 9 types of ground objects.  These include trees, Asphalt roads, Bricks, Meadows, etc., as shown in Table 1. Figure 2(a) is the pseudo-color image extracted from the three bands (80,60 and 20) and superimposed by the two-dimensional matrix as the three channels of the RGB image, and Figure 2(b) is the real ground object annotation map. There are altogether 9 feature categories, as shown in Table 1.  

 

 

 

 

 

 

 

 

(a) pseudo-color image (80,60,20)                                          (b) real ground object annotation map Figure 2 Pavia University data set

For hyperspectral image data, the number of labeled training sample points is different for each category, so the training set is selected in a certain proportion for each category, and the number of test set samples is 200.  Then different dimension reduction methods are used to reduce the training set and test set.  Finally, the SVM classifier was trained with the dimension reduction training set, and the SVM test was carried out with the dimension reduction test set. Finally, the classification accuracy of each dimension reduction method was obtained, which was repeated for 10 times to get the average value.  KPCA (Principal component analysis) method and SPCA-NMI method in literature Kefeng Li, Quanzhen Huang (2019) were selected for comparison with the method in this paper.  

 

Table 1 Features of Pavia University data set
The category number in the data set	Class name	the number of labeled training sample points
1	Asphalt	6631
2	Meadows	18649
3	Gravel	2099
4	Trees	3064
5	Painted metal sheets	1345
6	Bare Soil	5029
7	Bitumen	1330
8	Self-Blocking Bricks	3682
9	Shadows	947

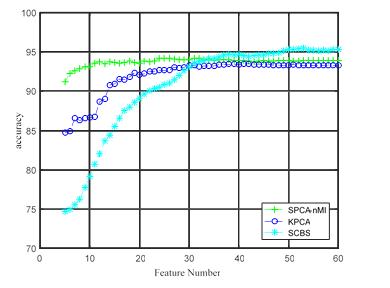
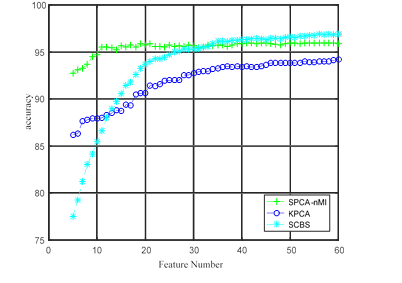
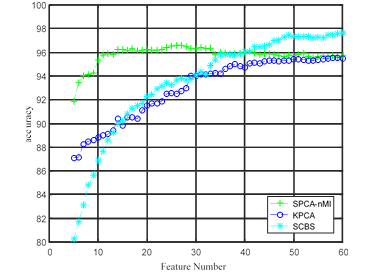
In the experiment, 5%, 10% and 15% labeled training sample points from each feature category were selected from the Pavia University data set to constitute the training set.  The dimensionality reduction feature number ranges from 5 to 60.  Three experimental results were obtained, as shown in Figure 3 (a) is the classification accuracy graph of 5% training sample set, Figure 3(b) is the classification accuracy graph of 10% training sample set, and Figure 3 (c) is the classification accuracy graph of 15% training sample set.  

 

(a) Classification accuracy graph of 5% training sample set

 

(b) Classification accuracy graph of 10% training sample set

 

(c) Classification accuracy graph for the 15% training sample set Figure 3 Relationship between feature number and SVM classification accuracy

 

 

It can be seen from the relation diagram of classification accuracy in Figure 3 that:

1)     The classification accuracy of all kinds of algorithms increases with the increase of the number of training samples. This is because the more training samples, the closer the support vector selected by the SVM classification model is to the classification boundary, and the better the classification hyperplane can be found, thus improving the classification accuracy.  

2)     The classification accuracy of SCBS method proposed in this paper is relatively low at the beginning, because SCBS is a feature selection method.  When the number of features is small, the discriminant ability of the features selected by the new method is limited, so the classification accuracy is low.  The other two methods are PAC-based data dimension reduction methods. The principal component selected by them represents the maximum variance direction of the original data, and integrates the discriminant ability of all features, so they can show high classification accuracy when the number of features is small.  However, with the increase of feature number, the classification accuracy based on PCA method improves slowly, and even slightly decreases, because the discriminant ability of the selected principal components is rapidly weakened, and the correlation between features is not taken into account, which leads to the decrease of classification accuracy.  The classification accuracy of SCBS method has been steadily improved.  After the feature number is greater than 30, SCBS gradually surpasses the other two algorithms.  It shows that the selected features of SCBS method gradually cover the representative feature sets, so the SCBS method has high discriminant ability.  Moreover, the subspace learning method can find the subspace embedded in the data and avoid the interference between the features, so the classification accuracy has been on the rise.  

 

5.    CONCLUSIONS

In order to solve the "dimensional disaster" problem of hyperspectral image data, a hyperspectral image classification method based on subspace clustering is proposed.  In the new method, the waveband images are regarded as data points. According to the self-representation characteristics, the sparse representation of each data point is established by solving a global sparse optimization problem, and then the similarity matrix between the data points is constructed.  Based on the similarity matrix, the spectral clustering algorithm is used to cluster the band images, and the cluster center of each class is selected as the representative band to form the band subset, and the hyperspectral pixel features are established by the band subset, and then the classification and recognition are carried out.  Experimental data show that the new method improves the accuracy of hyperspectral image classification.

 

 

 

 

REFERENCES

Anzhu Y U, Bing L, Zhipeng X. (2019) Salient Feature Extraction Method for Hyperspectral Image Classification. Acta Geodaetica et Cartographica Sinica. Retrieved          from https://doi.org/10.11947/j.AGCS.2019.20180499

 Feng Z, Yang S, Wang M. (2019) Learning Dual Geometric Low-Rank Structure for Semisupervised Hyperspectral Image Classification. IEEE Transactions on Cybernetics, (99),1-13. Retrieved          from https://doi.org/10.1109/TCYB.2018.2883472

 Fuding Xie, Cunkuan Lei, Fangfei Li. (2019) Unsupervised Hyperspectral Feature Selection based on Fuzzy C-means and Grey Wolf Optimizer. International Journal of Remote Sensing, 40(9),3344-3367. Retrieved          from https://doi.org/10.1080/01431161.2018.1541366

 Gao Q, Lim S, Jia X. (2019) Spectral-Spatial Hyperspectral Image Classification Using a Multiscale Conservative Smoothing Scheme and Adaptive Sparse Representation. IEEE Transactions on Geoscience and Remote Sensing, (99),1-13. Retrieved          from  https://doi.org/10.1109/TGRS.2019.2915809

 He N, Paoletti M E, Juan Mario Haut (2019). Feature Extraction With Multiscale Covariance Maps for Hyperspectral Image Classification. IEEE Transactions on Geoscience & Remote Sensing, 57(2),755-769. Retrieved          from https://doi.org/10.1109/TGRS.2018.2860464

Jiang X. Linear (2011) Subspace Learning-Based Dimensionality Reduction. IEEE Signal Processing Magazine, 28(2),16-26. Retrieved          from https://doi.org/10.1109/MSP.2010.939041

Kefeng Li, Quanzhen Huang (2019). Cross-pose Face Recognition by Integrating Regression Iteration and Interactive Subspace. Journal on Wireless Communications and Networking, (1),1-8. Retrieved          from https://doi.org/10.1186/s13638-019-1429-x

Md Rashedul Islam, Boshir Ahmed, Md Ali Hossain (2019). Feature Reduction Based on Segmented Principal Component Analysis for Hyperspectral Images Classification. International Conference on Electrical, Computer and Communication Engineering (ECCE). IEEE, 2019. Retrieved          from https://doi.org/10.1109/ECACE.2019.8679394

Ren R, Bao W. (2019) Hyperspectral Image Classification Based on Belief Propagation with Multi-features and Small Sample Learning. Journal of the Indian Society of Remote Sensing, 47(5),1-10. Retrieved          from https://doi.org/10.1007/s12524-018-00934-y

Venkatesan R, Prabu S. (2019) Hyperspectral Image Features Classification Using Deep Learning Recurrent Neural Networks. Journal of Medical Systems, 43(7). Retrieved          from https://doi.org/10.1007/s10916-019-1347-9

Wang A, Wang Y, Chen Y (2019). Hyperspectral Image Classification based on Convolutional Neural Network and Random Forest. Remote Sensing Letters, 10(11),1086-1094. Retrieved          from https://doi.org/10.1080/2150704X.2019.1649736

Wei Li, Yan Huang, C.-C (2017). Jay Kuo. Video-Based Human Motion Capture Data Retrieval via Normalized Motion Energy Image Subspace Projections. IEEE International Conference on Multimedia and Expo (ICME) Worksohp on Emerging Multimedia Systems and Applications. IEEE,1-7. Retrieved          from https://doi.org/10.1109/ACCESS.2020.3030258

Xiangpo Wei, Xuchu Yu, Bing Liu (2019). Convolutional Neural Networks and Local Binary Patterns for Hyperspectral Image Classificatio. European Journal of Remote Sensing, 52(1),448-462. Retrieved          from https://doi.org/10.1080/22797254.2019.1634980

Zhang J, Li C G, You C (2019). Self-Supervised Convolutional Subspace Clustering Network, CVPR,1-10. Retrieved          from https://doi.org/10.1109/CVPR.2019.00562

Zhao W, Du S. (2016) Spectral-Spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Transactions on Geoscience and Remote Sensing, , 54(8),4544-4554. Retrieved          from https://doi.org/10.1109/TGRS.2016.2543748