VALIDATION OF Σ−Y_LIQ ATOMIZATION MODEL IN PRESSURE SWIRL ATOMIZER

 

Sherry K. Amedorme ¹, NR.N. Roselina ²

 

¹ Department of Mechanical and Automotive Technology, Akenten Appiah-Menka University of Skills Training and Entrepreneurial Development, Kumasi-Ghana

² Faculty of Mechanical Engineering, Universiti Teknologi MARA, 40450 Shah Alam Selangor Malaysia

 

1. INTRODUCTION

Pressure swirl atomizer also known as simplex atomizers are of different types ranging from plain orifice to dual orifice atomizers. The fundamental principle of this atomizer is that liquid is induced in the tangential ports and the combination of the swirling and the translation motion of the liquid result in the liquid leaving the exit orifice as a hollow cone sheet with the formation of air core in the centre. The hollow cone sheet disintegrates into ligaments and then forms droplets  Lefebvre et al. (2017), Rashad et al. (2016), Cui et al. (2017). Liu et al. (2019) and Malý et al. (2018) studied the motion of liquid in the pressure swirl atomizer and indicate that the flow mechanism inside and outside the atomizer is complex and not well understood. Amongst several causes, factors such as the operating condition, design, and size of the atomizer tested, complex atomization process, as well as limitations of drop measurement instrument and techniques are very key considerations. In terms of design, the pressure atomizer has inlet ports, swirl chamber, and an outlet orifice.  The tangential inlet ports are of several channels and designs and introduce liquid fuel to the swirl chamber which imparts swirl energy to the liquid fuel and also contains air-core vortex. In this chamber, a portion of the swirl motion of the liquid is converted to axial velocity for the liquid to emerge as a hollow cone spray. The outlet orifice has contraction or convergence and contains holes for the liquid to be discharged Dafsari et al. (2017), Liu et al. (2017).

In these parts of the pressure swirl atomizer, the pressure exerted on the wall by the liquid, the tangential and the axial components of the velocity, and air-core characteristics are some of the important parameters analysed. These parameters significantly affect the discharge coefficient at the exit orifice, mean droplet sizes and distribution, spray cone angle, velocity distributions, and the liquid film thickness of the spray emanating from the atomizer. Several researchers including, Hu et al. (2019) and Wu et al. (2020), Shin et al. (2019), Ortman and Lefebvre (1985), and  Zhang et al. (2017) and Dafsari et al. (2019) studied the influence of injection pressure on spray cone angle. The results obtained show that within a given range of injection pressures, the equivalent spray angle is inversely related to the change in pressure. Ortman and Lefebvre also show that starting from atmospheric pressure, the spray cone angle first widens and then contracts with increases in the liquid pressure. The most common research on a pressure-swirl atomizer is the influence of pressure on the mean drop size. Several researchers including Lefebvre and Wang (1987), Belhadef et al. (2012), and Emekwuru and Watkins (2010) did extensive work in this regard. They show that the mean drop sizes emanating from the pressure-swirl atomizer decrease with increasing pressure. It is also observed that within the swirl chamber the pressure is constant but decreases sharply in both the convergence zone and the outlet orifice. The liquid velocity which has axial, tangential, and longitudinal components also depend mainly on the injection pressure and affect the degree of atomization Khani et al. (2020). The internal characteristics and the nozzle dimensions are not the only factors that govern atomization performance. Other factors relating to the liquid and ambient gas properties also affect greatly the mean droplet size and distribution. The instabilities and break-up of the liquid sheet are promoted by the gas density due to aerodynamic interaction but prevented by the liquid properties such as surface tension and viscosity. The ambient gas varies widely in pressure and temperature and influences strongly the mean droplet sizes and the spray angle. it is indicated that the ambient gas increases with decreasing spray angle until a maximum spray value is reached which does not affect the spray angle. Due to the higher inertia of the liquid phase, liquid density also alters the performance of the atomizer and the atomization characteristics, and it has been shown that its effect on the mean droplet size is quite minimal Lefebvre and McDonell (2017). In many studies, the liquid viscosity is the most important liquid property analysed in this atomizer. As indicated by Lefebvre although its influence on atomization is not that significant as the surface tension, however, its relevance is because it does not only influence the mean drop size and distribution but flow rate and the spray formation as well.  A key effect of increase in liquid viscosity is its reduction influence on the Reynolds number and the prevention of liquid sheet natural instability and break up. The overall effect is that it delays the disintegration of the liquid jet or sheet and increases the droplet sizes in the spray.

However, in a pressure swirl atomizer, a slight rise in the viscosity maximizes the flow rate which is achieved by increasing the liquid film thickness in the discharge orifice which in turn makes the effective flow area to be raised. But beyond the optimal liquid viscosity, this trend changes and the flow rate reduce with increase in liquid. The liquid flow rate does not only depend on the liquid properties but also on the geometrical sizes and the pressure difference across the atomizer Wimmer and Brenn (2012). Beheshti et al. (2007) assessed Ʃ −Y model in an air-assisted atomizer and predicted the effects of liquid properties and injection regimes on the atomization quality It was shown that the model predictions and experimental data have a good agreement for a wide range of variations of density and surface tension of the liquid as well as the injection regimes for liquid and gas jet exit velocities. They noted however that the model is limited in the fact that it only attempts to resolve the Sauter mean diameter (SMD) and as such is unable to resolve effects caused by a wide distribution of droplet size in polydispersed sprays such as ballistic drop spreading. They concluded that this is acceptable in the current application because existing experimental data for gaseous and aerosol jets show a lower spreading rate for an increasingly heavy central jet suggesting that variable density effects are more dominant than ballistic spreading Gharbi et al. (1996), Trask (2010), Beheshti et al. (2007).

In modelling two-phase flow in pressure swirl atomizers using computational fluid dynamics (CFD) two approaches are commonly used. The Eulerian approach where the spray is treated as a continuum within the computational flow domain and the Lagrangian technique tracked the droplets in the flow domain. Lin et al. (2009) and Xiong et al. (2009) carried out a study on non-swirling effervescent atomization spray using a combination of a Eulerian k-ɛ turbulence model to capture the droplets and gas-phase interaction in the secondary break-up and use the Lagrangian approach to model the disperse droplet phase. In this study, the droplet velocity is calculated in a far-field using a single-phase approach developed for high-density variation. In using the Eulerian method to solve two-phase problems the state equations of each phase are solved and the interaction between the two phases must be accounted for. This requires complex modelling and a high number of equations as each fluid is transported Bishop (1975), Drew (1983), Mirjalili et al.  (2017). This work focuses on the entirely one-fluid Eulerian model which potentially brings the advantage to compute only the transport of one single fluid with a high-density variation Belhadef et al. (2012). This novel and general mathematical model developed and presented by  Vallet et al.  (2001) for an entirely Eulerian model called the Ʃ-Y atomization model has the potential for all the basic necessary capabilities. It describes atomization from the first principle. However, its validation in pressure swirl atomizer is insufficient and has not been demonstrated well enough at the time being and therefore needs further research and improvement.

 

2. MATERIALS AND METHODS

The experiment was performed using the Malvern Spraytec drop measuring instrument as shown in Figure 1.  Liquid water in 0.4l container was pumped to the mainline with the aid of a 240V power source. The speed of the pump was controlled by a 300W triple source which enables the supply voltage to be varied. In measuring the mean droplet sizes at the various flow rate, the voltage supplied to the pump was varied since the flow rate could not be measured directly. The voltages of 0.5, 1, 1.5, 2 and 2.5 were used.  The pressure transducer was used to measure pressure drop across the apparatus and the pressure in the system is detected by a pressure sensor which converts it to an analogue signal to be read by the digital multimeter which then changes back to pressure. The circuit set up for the pressure measurement apparatus was in the range of 4-20mA containing a 500Ω resistor. The designed atomizer was clamped to a vertical stand to allow easy changing, and the liquid was sprayed downwards into the laser beam. The stand was built to accommodate variations in all directions above the laser beam. To prevent the deflection and splashback of the liquid absorbent tissue paper was put in the container.

Figure 1

                                                                     

Figure 1 Experimental Setup

 

The PFS 1392B1 atomizer used was produced by PNR Ltd which is a nozzle manufacturing company based in the UK. The specifications of the atomizer are inlet and exit diameters of 3.7 and 3.5mm respectively with a rated spray angle of 70 degrees and 3.90 per minute as flow rate at 3.0 bar gauge pressure as shown in Table 1. Liquid water was used for the experiment with density, viscosity property values as 1000 kg/m³, 0.001kg/ms, and 0.072 kg/s² respectively Crowley et al. (1990) Emekwuru and Watkins (2010).  The parameters of the Malvern instrument are shown in Table 2.

Table 1

Table 1 Atomizer Specification
Material	Atomizer length L (mm)	Height H (mm)	Atomizer Exit diameter (mm)	Liquid Inlet diameter (mm)
Stainless steel	34	24	3.5	3.7

 

Table 2

Table 2 Spraytec Specification Malvern-Instruments (2007)
Parameter	Value
Laser power	Max 4mW He-Ne Laser,
Data acquisition rate	10kHz- Rapid mode 1Hz-Continuous mode
Measurement Time	30 seconds - Rapid mode 60 minutes -Continuous mode
Lens Focal Length	300mm and 750mm
System Power	100/240v, 50/60 Hz
Mean drop size range	0.1-2500 um

 

3. RESULTS AND DISCUSSIONS

Figure 2 shows the graph of turbulent intensity decays along the axial position by comparing the standard k-epsilon and RNG k-epsilon turbulence models. It can be observed that the standard k-epsilon model predicted a higher decay in the average turbulent intensity as compared to RNG k-epsilon. In comparing the two   turbulence models, the inlet turbulent intensity was kept constant. In theory, turbulence is affected by swirl in the mean flow. Since the RNG model accounts for this rotational motion appropriately by modifying the turbulent viscosity, larger decay could be counted for and therefore the turbulence in the flow gets uniformly distributed in the swirl chamber and the computational domain as compared to the standard   model. In Figure 3, it can be seen that 10% of turbulent intensity is nearer to the experimental data points and the standard k-epsilon model utilize in this atomization is the best because it tends to produce the smallest SMD and the best match and configurations with the experimental results when compared to the RNG and Realizable K-epsilon turbulence models (Figure 4). It is observed that the turbulent intensity is greater in the periphery of the spray than the center spread of the nozzle, and this conforms to the observation made by Yoon et al. (2011). This is due to the droplet which decreases momentum in the outside spray making an enormous impact by the inflow of surrounding air. Towards the downstream of the spray, the turbulent intensity gets smaller because the momentum of relative velocity is sharply reduced and there are less actions of air current for droplet which is related with the highly small amount of air brought by its surroundings. However, there were no significant changes in the droplet velocity when the three turbulent models were compared as shown in Figure 5.

Figure 2

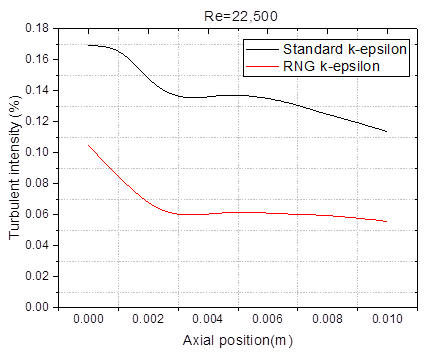
Figure 2 Turbulent Intensity Decays Along the Axial Position by Comparing the Standard and RNG K-Ε Turbulence Models

 

Figure 3

Figure 3 Effect of Turbulent Intensity on SMD

 

Figure 4

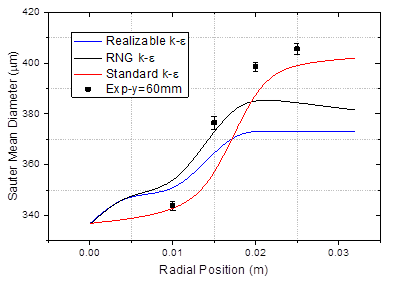
Figure 4 Effect of Turbulence Models on SMD at y=60mm

 

Figure 5

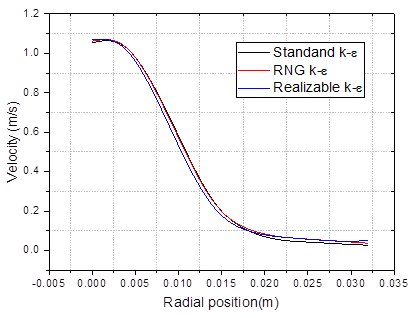
Figure 5 Influence of Turbulence Models on the Mean Liquid Velocity, Modelling

 

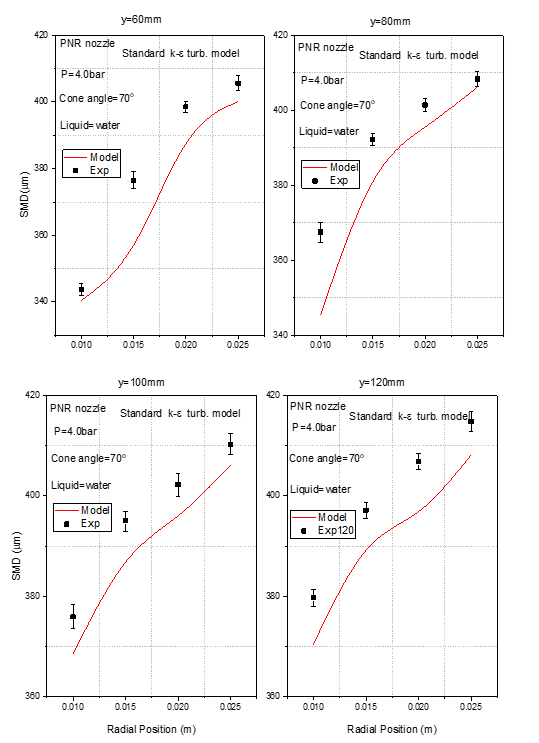
Figure 6 shows the comparison of the model with measurements for droplet Sauter Mean Diameter (SMD) at y=60, 80, 100 and 120 mm. The agreement between the model and experimental radial profiles at 60 mm downstream of the nozzle is good. The trend shows that the Sauter mean diameter SMD increases with increasing radial distances which is qualitatively correct, but the rate of change is small with the mean diameter of the large droplets found on the periphery of the spray under-predicted and the small mean drop size at the vicinity of the spray centreline perfectly predicted. At the axial position of 80 mm from the exit of the nozzle, the agreement between the atomisation model and experimental radial droplet mean diameter distributions is satisfactory with good prediction of the droplet size at the spray periphery but higher than the value predicted at position 60 mm axial distance from the nozzle exit. The rate of increase of droplet size with radial distance is correct and the size of the largest droplet at the spray periphery is well predicted. There is also a good agreement between the radial positions at 100 mm downstream of the nozzle for the model and the measurement with the droplet SMD having a slight under-prediction of less than an average of 3%. The result at this axial position also shows that most of the predicted SMDs near the inner region of the spray are below the experimental values. In addition, the SMD increases at similar rates with radial distances for both results at this axial position. The radial profiles for the mean droplet sizes (SMDs) between the calculations and the experiments at the axial position 120 mm from the exit of the nozzle are closer with the SMD being small near the centreline of the spray and SMD reasonably predicted. The trend of increasing droplet size with radial distance is observed and agrees with the work of many researchers in predicting the mean drop sizes from a pressure swirl atomizer Lefebvre and Wang (1987), Emekwuru and Watkins (2010). The mean drop diameter of the experimental results of the largest droplet at the periphery of the spray is higher than its predicted values. However, the SMD at a radial distance near the spray centreline is closely predicted in relation to the measurements. The more uniform and continuously increasing Sauter mean diameter with radial distance may be attributed to the farthest axial distance from which the drop sizes were measured and may also be due to the coalescence of smaller droplets and this has been accounted for in the model. The small drop sizes observed around the spray symmetry axis may be attributed to collisions between the liquid droplets and aerodynamic drag interactions with the entrained air as a result of the hollow cone spray pattern emanating from the nozzle Lefebvre and Wang (1987). The collisions result in unstable interactions between the drops and in turn lead to the breaking down of droplets smaller than their original sizes. This is also supported by the observation made by Yoon et al. (2011) that the separation of small droplets near the centreline arises due to the complex interaction between fluctuating turbulent length scales and air entrainment. This causes the mean gas motion to drive the smaller droplets towards the centreline of the spray. Larger droplets follow more ballistic trajectories subject to initial velocity vectors resulting from the liquid sheet breakup process and turbulent dispersion since they are not affected much by the air entrainment. However, in the downward part of the spray, the inward entrainment velocities are decreased to the point where smaller droplets are significantly dispersed from the centre line. Overall, the computational predictions of SMD for atomisation model shows a very good agreement with most of the experimental measurements in the radial positions when standard k-ɛ turbulence was used. However, more divergence  was observed between the predictions and the experimental measurements when the RNG k-ɛ turbulence model and Realizable k-ɛ turbulence model were  used in the predictions as  shown  in Figure 7 and Figure 8.

Figure 6

                                                               

Figure 6 Validation of Droplet SMD, Model with Experiment, Standard k-ɛ Turbulence Model

 

 

Figure 7

                                                                    

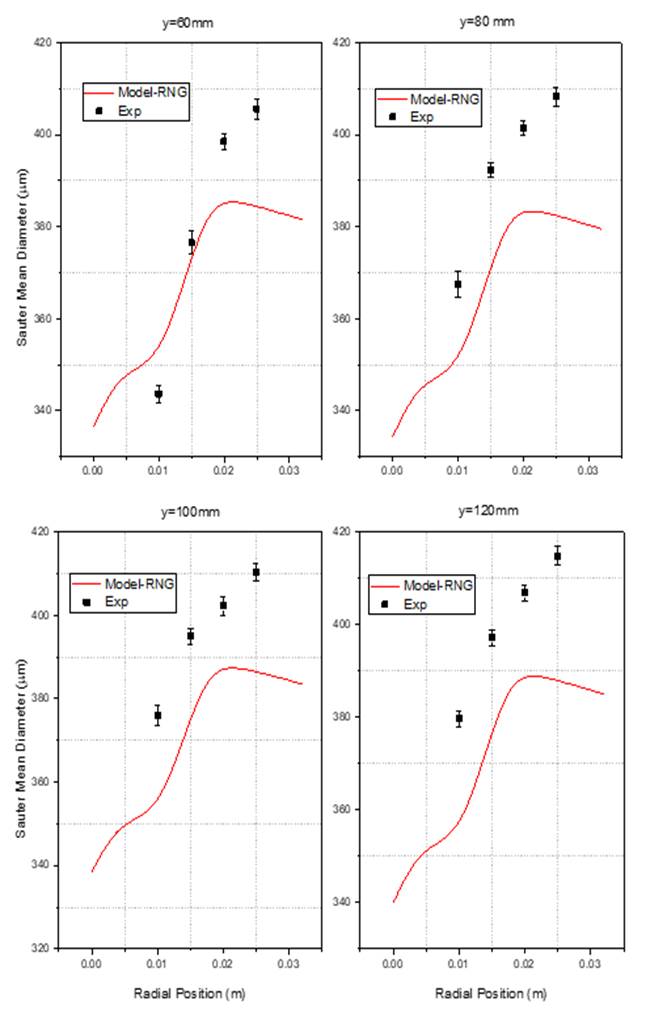
Figure 7 Validation of Droplet SMD, Model with Experiment, RNG k-ɛ Turbulence Model

 

Figure 8                                         

                                                                       

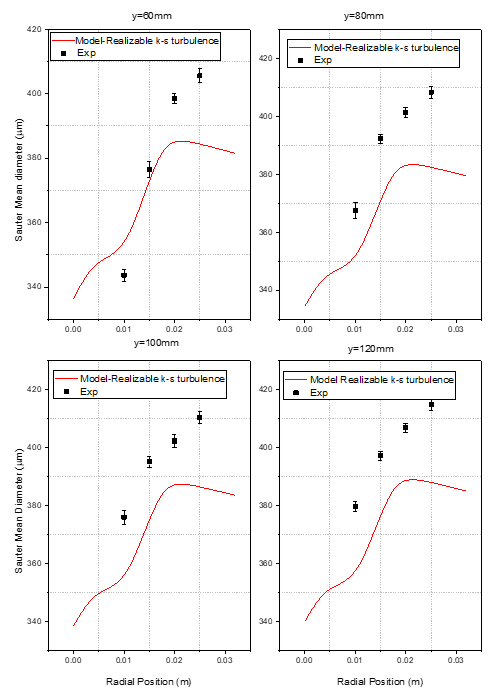
Figure 8 Validation of Droplet SMD, Model with Experiment, Realizable k-ɛ Turbulence Model

 

Figure 9 illustrates the validation of the model with the experimental results on the spray centreline. It can be observed that the model has good agreement with the measurements with a percentage error of less than an average of 5% between the model and the experiments at axial distances of 60 mm and 120mm. Better predictions are observed at axial distances 80mm and 100mm. Figure 10 shows more clearly how sensitive SMD is to the pressure differentials. This is because as pressure increases the faster maximum growth rate of the liquid film occurs and will lead to the linear stability of the surface wave of the thread film getting worse. So, the interaction between the liquid phase and the gas phase becomes stronger and the film can break up more easily. This will make the droplet SMD get smaller as pressure increases.

Figure 9

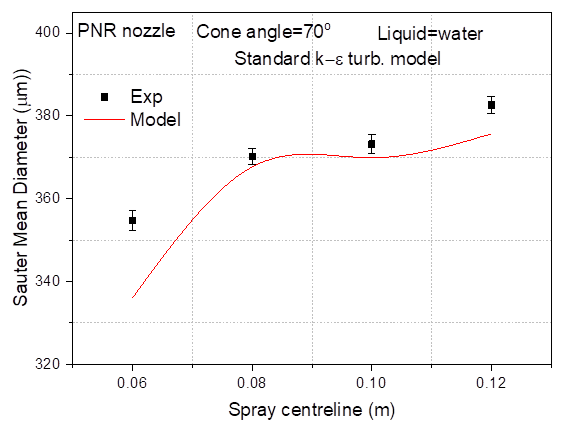
Figure 9 Validation of SMD at Spray Centre Axis, Model, and Experiment

 

Figure 10

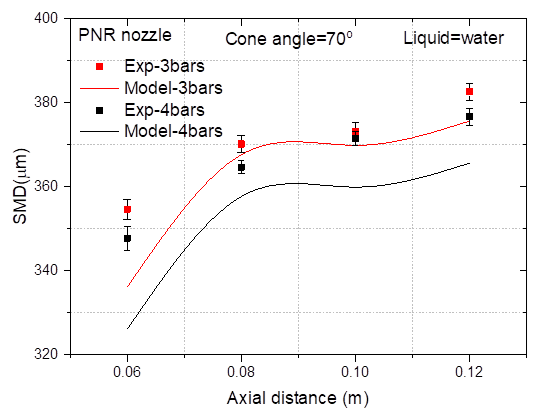
Figure 10 Effect of Pressure on SMD, Model and Experiment

 

4. CONCLUSIONS

A validation of mean drop sizes at both centreline and radial positions was performed using laser-diffraction-based drop size measurement and atomization model. It is shown that the model predictions have good agreement with the experimental measurements when standard k-ɛ turbulence was used. The experimental results are also consistent with the model predictions when the effect of pressure differential on the SMD was analysed. In all, it can be concluded that the computational predictions of SMD for the atomization model shows good validation with the experimental measurements.

 

CONFLICT OF INTERESTS

None. 

 

ACKNOWLEDGMENTS

None.

 

REFERENCES

Beheshti, N., Burluka, A. A., and Fairweather, M. (2007). Assessment of Σ− Y liq Model Predictions for Air-Assisted Atomisation. Theoretical and Computational Fluid Dynamics, 21, 381-397. https://doi.org/10.1007/s00162-007-0052-3.

Belhadef, A., Vallet, A., Amielh, M., and Anselmet, F. (2012). Pressure-Swirl Atomization : Modeling and Experimental Approaches. International Journal of Multiphase Flow, 39, 13-20. https://doi.org/10.1016/j.ijmultiphaseflow.2011.09.009.  

Bishop, R. (1975). Thermo-Fluid Dynamic Theory of Two-Phase Flow. IOP Publishing. https://doi.org/10.1088/0031-9112/26/12/034.  

Crowley, J. M., Wright, G. S., and Chato, J. C. (1990). Selecting a Working Fluid to Increase the Efficiency and Flow Rate of an EHD Pump. IEEE Transactions on Industry Applications, 26(1), 42-49. https://doi.org/10.1109/28.52672.  

Cui, J., Lai, H., Li, J., and Ma, Y. (2017). Visualization of Internal Flow and the Effect of Orifice Geometry on the Characteristics of Spray and Flow Field in Pressure-Swirl Atomizers. Applied Thermal Engineering, 127, 812-822. https://doi.org/10.1016/j.applthermaleng.2017.08.103.  

Dafsari, R. A., Lee, H. J., Han, J., Park, D. C., and Lee, J. (2019). Viscosity Effect on the Pressure Swirl Atomization of an Alternative Aviation Fuel. Fuel, 240, 179-191. https://doi.org/10.1016/j.fuel.2018.11.132.  

Dafsari, R. A., Vashahi, F., and Lee, J. (2017). Effect of Swirl Chamber Length on the Atomization Characteristics of a Pressure-Swirl Nozzle. Atomization and Sprays, 27(10), 859-874. https://doi.org/10.1615/AtomizSpr.2017024777.  

Drew, D. A. (1983). Mathematical Modeling of Two-Phase Flow. Annual Review of Fluid Mechanics, 15, 261-291. https://doi.org/10.1146/annurev.fl.15.010183.001401.  

Emekwuru, N., and Watkins, A. P. (2010). Analysis of a Two-Fluid Sprayer and its Use to Develop the Number Size Distribution Moments Spray Model, Part II :Computational Analysis. Atomization and Sprays, 20(6), 467-484. https://doi.org/10.1615/AtomizSpr.v20.i6.10.  

Gharbi, A., Ruffin, A., Anselmet, F., and Schiestel, R. (1996). Numerical Modelling of Variable Density Turbulent Jets. International Journal of Heat and Mass Transfer, 39(9), 1865-1882. https://doi.org/10.1016/0017-9310(95)00290-1.  

Hu, J., Liu, B., Zhang, C., Gao, H., Zhao, Z., Zhang, F., Wang, Y. (2019). Experimental Study on the Spray Characteristics of an Air-Assisted Fuel Injection System Using Kerosene and Gasoline. Fuel, 235, 782-794. https://doi.org/10.1016/j.fuel.2018.08.083.  

Khani Aminjan, K., Kundu, B., and Ganji, D. (2020). Study of Pressure Swirl Atomizer with Tangential Input at Design Point and Outside of Design Point. Physics of Fluids, 32(12), 127113. https://doi.org/10.1063/5.0032174.  

Lefebvre, A. H., and McDonell, V. G. (2017). Atomization and Sprays. CRC press. https://doi.org/10.1201/9781315120911.  

Lefebvre, A., and Wang, X. (1987). Mean Drop Sizes from Pressure-Swirl Nozzles. Journal of Propulsion and Power. 3(1), 11-18. https://doi.org/10.2514/3.22946.  

Lin, J., Qian, L., Xiong, H., and Chan, T. L. (2009). Effects of Operating Conditions on Droplet Deposition onto Surface of Atomization Impinging Spray. Surface and Coatings Technology, 203(12), 1733-174. https://doi.org/10.1016/j.surfcoat.2009.01.009.  

Liu, C., Liu, F., Yang, J., Mu, Y., Hu, C., and Xu, G. (2019). Experimental Investigations of Spray Generated by a Pressure Swirl Atomizer. Journal of the Energy Institute, 92(2), 210-221. https://doi.org/10.1016/j.joei.2018.01.014.  

Liu, Z., Huang, Y.,  and Sun, L. (2017). Studies on Air Core Size in A Simplex Pressure-Swirl Atomizer. International Journal of Hydrogen Energy, 42, 18649-18657. https://doi.org/10.1016/j.ijhydene.2017.04.188.  

Malvern-Instruments (2007). Spraytec User Manual MAN0368. Issue.

Malý, M., Sapík, M., Jedelský, J., Janáčková, L., Jícha, M., Sláma, J., Wigley, G. (2018). Internal Flow Characteristics in Scaled Pressure-Swirl Atomizer. EPJ Web of Conferences. 02059. https://doi.org/10.1051/epjconf/201818002059.  

Mirjalili, S., Jain, S. S., and Dodd, M. (2017). Interface-Capturing Methods for Two-Phase Flows : An Overview and Recent Developments. Center for Turbulence Research Annual Research Briefs, 117-135.

Ortman, J., and Lefebvre, A. (1985). Fuel Distributions from Pressure-Swirl Atomizers. AIAA Journal of Propulsion and Power, 1(1), 11-15. https://doi.org/10.2514/3.22752.  

Rashad, M., Yong, H., and Zekun, Z. (2016). Effect of Geometric Parameters on Spray Characteristics of Pressure Swirl Atomizers. International Journal of Hydrogen Energy, 41(35), 15790-15799.  https://doi.org/10.1016/j.ijhydene.2016.04.037.  

Shin, D., Bokhart, A. J., Rodrigues, N. S., Sojka, P., Gore, J. P., and Lucht, R. P. (2019). Experimental Study of Spray Characteristics at Cold Start and Elevated Ambient Pressure Using Hybrid Airblast Pressure-Swirl Atomizer.  AIAA Scitech 2019 Forum, 1737. https://doi.org/10.2514/6.2019-1737.  

Trask, N. A. (2010). Implementation of an Eulerian Atomization Model to Characterize Primary Spray Formation. Masters Theses, 434.

Vallet, A., Burluka, A.A., and Borghi, R. (2001). Development of a Eulerian Model for the "Atomization" of a Liquid Jet. Atomization and Sprays, 11(6). https://doi.org/10.1615/AtomizSpr.v11.i6.20.  

Wimmer, E., and Brenn, G. (2012). Viscous Effects on Flows Through Pressure-Swirl Atomizers. In Proceedings of the 12th Triennial International Conference on Liquid Atomization and Spray Systems (ICLASS 2012), Heidelberg, Germany. 2-6.

Wu, S., Gandhi, A., Li, H., and Meinhart, M. (2020). Experimental and Numerical Study of the Effects of Nozzle Taper Angle on Spray Characteristics of Gdi Multi-Hole Injectors at Cold Condition. Fuel, 275, 17888. https://doi.org/10.1016/j.fuel.2020.117888.  

Xiong, H. B., Lin, J. Z., and Zhu, Z. F. (2009). Three-Dimensional Simulation of Effervescent Atomization Spray. Atomization and Sprays, 19(1), 75-90. https://doi.org/10.1615/AtomizSpr.v19.i1.50.  

Yoon, S. H., Kim, D. K., and Kim, B. H. (2011). Effect of Nozzle Geometry for Swirl Type Twin-Fluid Water Mist Nozzle on the Spray Characteristic. Journal of Mechanical Science and Technology, 25, 1761. https://doi.org/10.1007/s12206-011-0506-9.  

Zhang, T., Dong, B., Chen, X., Qiu, Z., Jiang, R. and Li, W. (2017). Spray Characteristics of Pressure-Swirl Nozzles at Different Nozzle Diameters. Applied Thermal Engineering, 121, 984-991. https://doi.org/10.1016/j.applthermaleng.2017.04.089.